练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图1，是等边三角形，D.E分别是BC.AC上两点，且，与AD交于点H，链接CH.

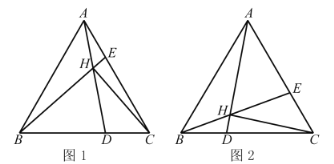
    （1）当时，求的值；

    （2）如图2，当时，__________； __________.

    【答案】（1）； （2）；.

    【解析】

    （1）根据题意可得，得出，证明四点共圆，连接，由圆周角定理得出得出

    ，作于则，得出，利用平行线的比例关系，结合边角关系，即可得出结果；

    （2）同（1）得：四点共圆，连接，由圆周角定理得出，

    ，得出，得出，作交于，则，得出，与（1）同理，可得出结论.

    （1）是等边三角形，

    ，

    ，

    ，

    四点共圆，连接，如图（1）所示，

    则，

    ，

    ，作于，

    则，

    ，

    设，则，在中，

    ，

    ；

    （2）同（1）得：四点共圆，连接，

    ，

    ，，

    作交于，则，，

    ，设，则，

    在中，，，

    .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知、、是平面上任意三点，且，，.则的最小值是______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了调查患胃病是否与生活不规律有关，在患胃病与生活不规律这两个分类变量的计算中，下列说法正确的是（ ）

    A. 越大，“患胃病与生活不规律没有关系”的可信程度越大.

    B. 越大，“患胃病与生活不规律有关系”的可信程度越小.

    C.若计算得 ，经查临界值表知 ，则在 个生活不规律的人中必有 人患胃病.

    D.从统计量中得知有 的把握认为患胃病与生活不规律有关，是指有 的可能性使得推断出现错误.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“石头、剪刀、布”是一种广泛流传于我国民间的古老游戏，其规则是：用三种不同的手势分别表示石头、剪刀、布；两个玩家同时出示各自手势次记为次游戏，“石头”胜“剪刀”，“剪刀”胜“布”，“布”胜“石头”；双方出示的手势相同时，不分胜负.现假设玩家甲、乙双方在游戏时出示三种手势是等可能的.

    （1）求在次游戏中玩家甲胜玩家乙的概率；

    （2）若玩家甲、乙双方共进行了次游戏，其中玩家甲胜玩家乙的次数记作随机变量，求的分布列及.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在盒子里有大小相同，仅颜色不同的乒乓球共10个，其中红球5个，白球3个，蓝球2个.现从中任取出一球确定颜色后放回盒子里，再取下一个球.重复以上操作，最多取3次，过程中如果取出蓝色球则不再取球.

    （1）求整个过程中恰好取到2个白球的概率；

    （2）求取球次数的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论函数的单调性；

    （2）设，若存在，使得不等式成立，求m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】上饶市在某次高三适应性考试中对数学成绩数据统计显示，全市10000名学生的成绩近似服从正态分布，现某校随机抽取了50名学生的数学成绩分析，结果这50名学生的成绩全部介于85分到145分之间，现将结果按如下方式分为6组，第一组，第二组，…，第六组，得到如图所示的频率分布直方图：

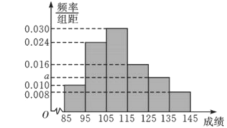
    （1）试由样本频率分布直方图估计该校数学成绩的平均分数；

    （2）若从这50名学生中成绩在125分（含125分）以上的同学中任意抽取3人，该3人在全市前13名的人数记为，求的概率.

    附：若，则，，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了提高学生的身体素质，某校高一、高二两个年级共名学生同时参与了“我运动，我健康，我快乐”的跳绳、踢毽等系列体育健身活动.为了了解学生的运动状况，采用分层抽样的方法从高一、高二两个年级的学生中分别抽取名和名学生进行测试.下表是高二年级的名学生的测试数据（单位：个/分钟）：

    学生编号

    1

    2

    3

    4

    5

    跳绳个数

    179

    181

    168

    177

    183

    踢毽个数

    85

    78

    79

    72

    80

    （1）求高一、高二两个年级各有多少人？

    （2）设某学生跳绳个/分钟，踢毽个/分钟.当，且时，称该学生为“运动达人”.

    ①从高二年级的学生中任选一人，试估计该学生为“运动达人”的概率；

    ②从高二年级抽出的上述名学生中，随机抽取人，求抽取的名学生中为“span>运动达人”的人数的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足：①（）；②当（）时，；③当（）时，，记数列的前项和为.

    （1）求，，的值；

    （2）若，求的最小值；

    （3）求证：的充要条件是（）.

    查看答案和解析>>

    同步练习册答案