
【题目】已知直线a、b和平面![]() ,下列说法中正确的有______ .
,下列说法中正确的有______ .
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若
若![]() ,则
,则![]() ;
;
![]() 若直线
若直线![]() ,直线
,直线![]() ,则
,则![]() ;
;
![]() 若直线a在平面
若直线a在平面![]() 外,则
外,则![]() ;
;
![]() 直线a平行于平面
直线a平行于平面![]() 内的无数条直线,则
内的无数条直线,则![]() ;
;
![]() 若直线
若直线![]() ,那么直线a就平行于平面
,那么直线a就平行于平面![]() 内的无数条直线.
内的无数条直线.
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且
,且![]() 在
在![]() 和
和![]() 处取得极值.
处取得极值.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)设函数![]() ,是否存在实数
,是否存在实数![]() ,使得曲线
,使得曲线![]() 与
与![]() 轴有两个交点,若存在,求出
轴有两个交点,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在半径为R的圆桌上摆放同样大小的半径为r的硬币.要求硬币不准露出圆桌面边缘,并且所摆硬币彼此不能重叠.当摆放n枚硬币之后,圆桌上就不能再多摆放一枚这种硬币了.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水葫芦原产于巴西,![]() 年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过
年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() ,经过
,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() . 现水葫芦覆盖面积
. 现水葫芦覆盖面积![]() (单位
(单位![]() )与经过时间
)与经过时间![]() 个月的关系有两个函数模型
个月的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(参考数据:![]() )
)
(Ⅰ)试判断哪个函数模型更合适,并求出该模型的解析式;
(Ⅱ)求原先投放的水葫芦的面积并求约经过几个月该水域中水葫芦面积是当初投放的![]() 倍.
倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某粮库拟建一个储粮仓如图所示,其下部是高为2的圆柱,上部是母线长为2的圆锥,现要设计其底面半径和上部圆锥的高,若设圆锥的高![]() 为
为![]() ,储粮仓的体积为
,储粮仓的体积为![]() .
.
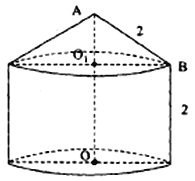
(1)求![]() 关于
关于![]() 的函数关系式;(圆周率用
的函数关系式;(圆周率用![]() 表示)
表示)
(2)求![]() 为何值时,储粮仓的体积最大.
为何值时,储粮仓的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
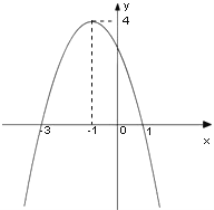
【题目】如图是一个二次函数y=f(x)的图象
(1)写出这个二次函数的零点
(2)求这个二次函数的解析式
(3)当实数k在何范围内变化时,函数g(x)=f(x)-kx在区间[-2,2]上是单调函数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过圆O外一点P作圆的切线PC,切点为C,割线PAB、割线PEF分别交圆O于A与B、E与F.已知PB的垂直平分线DE与圆O相切. 
(1)求证:DE∥BF;
(2)若 ![]() ,DE=1,求PB的长.
,DE=1,求PB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双曲线的方程为![]() ”是“双曲线的渐近线方程为
”是“双曲线的渐近线方程为![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】双曲线的方程为![]() ,则渐近线方程为
,则渐近线方程为![]() ,渐近线方程为:
,渐近线方程为: ![]() ,反之当渐近线方程为
,反之当渐近线方程为![]() 时,只需要满足
时,只需要满足![]() ,等轴双曲线即可.故选择充分不必要条件.
,等轴双曲线即可.故选择充分不必要条件.
故答案为:A.
【题型】单选题
【结束】
10
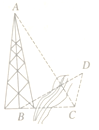
【题目】如图,为测量河对岸塔![]() 的高,先在河岸上选一点
的高,先在河岸上选一点![]() ,使
,使![]() 在塔底
在塔底![]() 的正东方向上,在点
的正东方向上,在点![]() 处测得
处测得![]() 点的仰角为
点的仰角为![]() ,再由点
,再由点![]() 沿北偏东
沿北偏东![]() 方向走
方向走![]() 到位置
到位置![]() ,测得
,测得![]() ,则塔
,则塔![]() 的高是( )
的高是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线相交于
与抛物线相交于![]() 两点,分别过点
两点,分别过点![]() 作抛物线的两条切线
作抛物线的两条切线![]() 和
和![]() ,记
,记![]() 和
和![]() 相交于点
相交于点![]() .
.
(1)证明:直线![]() 和
和![]() 的斜率之积为定值;
的斜率之积为定值;
(2)求证:点![]() 在一条定直线上.
在一条定直线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com