
 -ax2,a∈R.
-ax2,a∈R. ,x=
,x= ,x=
,x= (2)见解析(3)(1,+∞)
(2)见解析(3)(1,+∞) -2x2=0,即x(2x2+4x-1)=0,解得x=0或x=
-2x2=0,即x(2x2+4x-1)=0,解得x=0或x= (舍负);
(舍负); -2x2=0,
-2x2=0, .
. ,x=
,x= ,x=
,x= .
. -ax2=0,即ax2+2ax-1=0.
-ax2=0,即ax2+2ax-1=0. -ax2=0,即ax2+2ax+1=0(x≠-2).①
-ax2=0,即ax2+2ax+1=0(x≠-2).① =0(x≠-2),即x2+2x=-
=0(x≠-2),即x2+2x=- =0.
=0. <0,得a>1,
<0,得a>1,

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
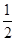 t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 上的零点个数为________.
上的零点个数为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.f(x)=2x+b,x∈R,x= |
| B.f(x)=ex,x∈R,x=cost |
| C.f(x)=x2,x∈R,x=et |
| D.f(x)=|x|,x∈R,x=lnt |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .若水晶产品的销售价格不变,第n次投入后的年利润为f(n)万元.
.若水晶产品的销售价格不变,第n次投入后的年利润为f(n)万元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com