
【题目】已知不等式![]() 的解集为
的解集为![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 的解集为
的解集为![]() ,不等式
,不等式![]() 的解集为
的解集为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)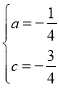 ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)利用一元二次不等式的解集与相应的一元二次方程的实数根的关系即可求出;(2)“![]() ”是“
”是“![]() ”的充分不必要条件,将它们对应的不等式分别解出,可得集合
”的充分不必要条件,将它们对应的不等式分别解出,可得集合![]() 从而建立关于
从而建立关于![]() 的不等关系,解关于
的不等关系,解关于![]() 不等式即可得到实数
不等式即可得到实数![]() 的取值范围.
的取值范围.
试题解析:(1)依题意得,1、3是方程![]() 的两根,且
的两根,且![]() ,...............1分
,...............1分
所以,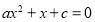 ............................. 3分
............................. 3分
解得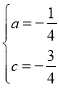 ;................... 5分
;................... 5分
(2)由(1)得![]() ,所以,
,所以,![]() 即为
即为![]() ,
,
解得,![]() ,∴
,∴![]() ,
,
又![]() ,即为
,即为![]() 解得
解得![]() ,∴
,∴![]() ,............8分
,............8分
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() ...............10分
...............10分


科目:高中数学 来源: 题型:
【题目】如图,一个铝合金窗分为上、下两栏,四周框架和中间隔档的材料为铝合金,宽均为6![]() ,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800
,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800![]() ,设该铝合金窗的宽和高分别为
,设该铝合金窗的宽和高分别为![]() ,铝合金窗的透光部分的面积为
,铝合金窗的透光部分的面积为![]() .
.
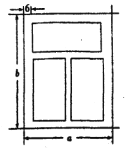
(1)试用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,则铝合金窗的宽和高分别为多少?
最大,则铝合金窗的宽和高分别为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在四棱锥![]() 中,底面
中,底面![]() 是正方形,
是正方形, ![]() .
.
(1)如图2,设点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)已知网格纸上小正方形的边长为![]() ,请你在网格纸上用粗线画图1中四棱锥
,请你在网格纸上用粗线画图1中四棱锥![]() 的府视图(不需要标字母),并说明理由.
的府视图(不需要标字母),并说明理由.
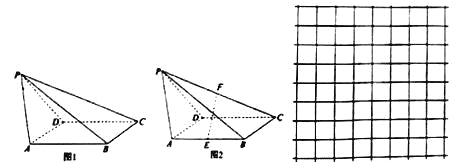
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了整顿食品的安全卫生,食品监督部门对某食品厂生产甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,下表是测量数据的茎叶图(单位:毫克).

规定:当食品中的有害微量元素的含量在![]() 时为一等品,在
时为一等品,在![]() 为二等品,20以上为劣质品.
为二等品,20以上为劣质品.
(1)用分层抽样的方法在两组数据中各抽取5个数据,再分别从这5个数据中各选取2个,求甲的一等品数与乙的一等品数相等的概率;
(2)每生产一件一等品盈利50元,二等品盈利20元,劣质品亏损20元,根据上表统计得到甲、乙两种食品为一等品、二等品、劣质品的频率,分别估计这两种食品为一等品、二等品、劣质品的概率,若分别从甲、乙食品中各抽取1件,设这两件食品给该厂带来的盈利为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 的面积最大时,求
的面积最大时,求![]() 的直线方程.
的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数).
为参数).
(I)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(II)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的![]() 倍,得到曲线
倍,得到曲线![]() .设点
.设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com