
【题目】在极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,现以极点
,现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,曲线
轴的非负半轴建立平面直角坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 为曲线
为曲线![]() 关于直线
关于直线![]() 的对称曲线,点
的对称曲线,点![]() 分别为曲线
分别为曲线![]() 、曲线
、曲线![]() 上的动点,点
上的动点,点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图所示,已知直线![]() 与双曲线
与双曲线![]() 交于A,B两点,且点A的横坐标为4.
交于A,B两点,且点A的横坐标为4.
(1)求![]() 的值及B点坐标;
的值及B点坐标;
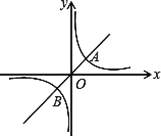
(2)结合图形,直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到100![]() ,水温
,水温![]() 与时间
与时间![]() 近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度
近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度![]() 与时间
与时间![]() 近似满足函数的关系式为
近似满足函数的关系式为 ![]() (
(![]() 为常数), 通常这种热饮在40
为常数), 通常这种热饮在40![]() 时,口感最佳,某天室温为
时,口感最佳,某天室温为![]() 时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为
时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为

A. 35![]() B. 30
B. 30![]()
C. 25![]() D. 20
D. 20![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),M为
为参数),M为![]() 上的动点,P点满足
上的动点,P点满足![]() ,点P的轨迹为曲线
,点P的轨迹为曲线![]() .
.
(I)求![]() 的方程;
的方程;
(II)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 的异于极点的交点为A,与
的异于极点的交点为A,与![]() 的异于极点的交点为B,求|AB|.
的异于极点的交点为B,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线![]() 的焦点重合,过点
的焦点重合,过点![]() 且不垂直于
且不垂直于![]() 轴的直线
轴的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为提高服务质量,随机调查了50名男顾客和50名女顾客,每位顾客对该商场的服务给出满意或不满意的评价,得到下面列联表:
满意 | 不满意 | |
男顾客 | 40 | 10 |
女顾客 | 30 | 20 |
(1)分别估计男、女顾客对该商场服务满意的概率;
(2)能否有95%的把握认为男、女顾客对该商场服务的评价有差异?
附:![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com