
如果函数 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。
(1)判断函数 是否具有“
是否具有“ 性质”,若具有“
性质”,若具有“ 性质”,求出所有
性质”,求出所有 的值;若不具有“
的值;若不具有“ 性质”,说明理由;
性质”,说明理由;
(2)已知 具有“
具有“ 性质”,且当
性质”,且当 时
时 ,求
,求 在
在 上有最大值;
上有最大值;
(3)设函数 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若 与
与 交点个数为2013,求
交点个数为2013,求 的值.
的值.
(1) 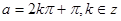 ,(2) 当
,(2) 当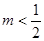 时,
时,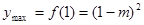 ,当
,当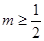 时,
时,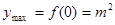 , (3)
, (3) 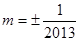 .
.
解析试题分析:(1)新定义问题,必须从定义出发,实际是对定义条件的直译. 由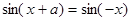 得
得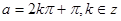 ,(2)由
,(2)由  性质知函数为偶函数. ∴
性质知函数为偶函数. ∴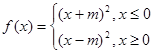 当
当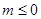 时,∵
时,∵ 在
在 单调增,∴
单调增,∴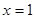 时,
时,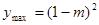 ,当
,当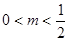 时,∵
时,∵ 在
在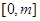 单调减,在
单调减,在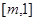 上单调增,又
上单调增,又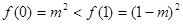 ,∴
,∴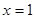 时,
时,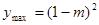 ,当
,当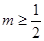 时,∵
时,∵ 在
在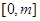 单调减,在
单调减,在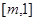 上单调增,又
上单调增,又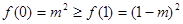 ,∴
,∴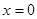 时,
时,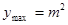 . (3) ∵函数
. (3) ∵函数 具有“
具有“ 性质” ∴
性质” ∴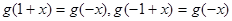 ∴
∴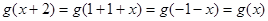 ∴函数
∴函数 是以2为周期的函数. 当
是以2为周期的函数. 当 时,
时, 为偶函数,因此易得函数
为偶函数,因此易得函数 是以1为周期的函数.结合图像得: ①当
是以1为周期的函数.结合图像得: ①当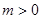 时,要使得
时,要使得 与
与 有2013个交点,只要
有2013个交点,只要 与
与 在区间
在区间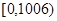 有2012个交点,而在
有2012个交点,而在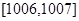 内有一个交点∴
内有一个交点∴ 过
过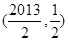 ,从而得
,从而得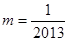 ,②当
,②当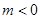 时,同理可得
时,同理可得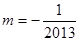 ,③当
,③当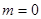 时,不合题意, 综上所述
时,不合题意, 综上所述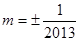 .
.
(1)由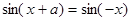 得
得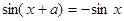
∴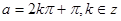
∴函数 具有“
具有“ 性质”,其中
性质”,其中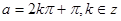 2分
2分
(2) ∵ 具有“
具有“ 性质”
性质”
∴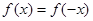
设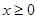 ,则
,则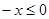 ,∴
,∴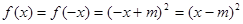
∴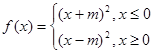 4分
4分
当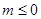 时,∵
时,∵ 在
在 单调增,∴
单调增,∴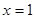 时,
时,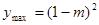 5分
5分
当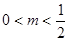 时,∵
时,∵

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知函数 a为常数且a>0.
a为常数且a>0.
(1)证明:函数f(x)的图像关于直线x= 对称;
对称;
(2)若x0满足f(f(x0))= x0,但f(x0)≠x0,则x0称为函数f(x)的二阶周期点,如果f(x)有两个二阶周期点x1,x2,试确定a的取值范围;
(3)对于(2)中的x1,x2,和a,设x3为函数f(f(x))的最大值点,A(x1,f(f(x1))),B(x2,f(f(x2))),C(x3,0),记△ABC的面积为S(a),讨论S(a)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路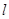 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为 .
.
(1)当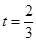 时,求直路
时,求直路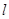 所在的直线方程;
所在的直线方程;
(2)当t为何值时,地块OABC在直路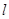 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数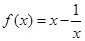 ,
,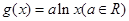 .
.
(1)a≥-2时,求F(x)=f(x)-g(x)的单调区间;
(2)设h(x)=f(x)+g(x),且h(x)有两个极值点为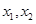 ,其中
,其中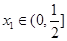 ,求
,求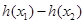 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com