
【题目】已知各项均为整数的数列{an}中,a1=2,且对任意的n∈N* , 满足an+1﹣an<2n+ ![]() ﹣1,则a2017= .
﹣1,则a2017= .
【答案】22017
【解析】解:由满足an+1﹣an<2n+ ![]() ,
,
∴an+2﹣an+1<2n+1+ ![]() ,∴an+2﹣an<3×2n+1.
,∴an+2﹣an<3×2n+1.
又an+2﹣an>3×2n﹣1.
∴an+2﹣an=3×2n.
∴a2017=(a2017﹣a2015)+(a2015﹣a2013)+…+(a3﹣a1)+a1
=3×22015+3×22013+…+3×21+2
=3× ![]() +2
+2
=22017.
故答案为:22017.
由满足an+1﹣an<2n+ ![]() ,可得 an+2﹣an+1<2n+1+
,可得 an+2﹣an+1<2n+1+ ![]() ,根据同向不等式可加的性质可得 an+2﹣an<3×2n+1,结合n+2﹣an>3×2n﹣1,不难得出an+2﹣an=3×2n,使用叠加可得答案.
,根据同向不等式可加的性质可得 an+2﹣an<3×2n+1,结合n+2﹣an>3×2n﹣1,不难得出an+2﹣an=3×2n,使用叠加可得答案.


科目:高中数学 来源: 题型:
【题目】已知PC⊥平面ABC,AC=2 ![]() ,PC=BC,AB=4,∠BAC=30°. 点D是线段AB上靠近B的四等分点,PE∥CB,PC∥EB.
,PC=BC,AB=4,∠BAC=30°. 点D是线段AB上靠近B的四等分点,PE∥CB,PC∥EB.
(Ⅰ)证明:直线AB⊥平面PCD;
(Ⅱ)若F为线段AC上靠近C的四等分点,求平面PDF与平面CBD所成锐二面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.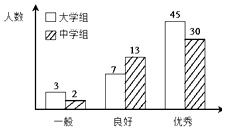
(Ⅰ)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:K2 ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(k2≥k0) | 0.10 | 0.05 | 0.005 |
k0 | 2.706 | 3.841 | 7.879 |
(Ⅱ)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;
(Ⅲ)如果在优秀等级的选手中取4名,在良好等级的选手中取2名,再从这6人中任选3人组成一个比赛团队,求所选团队中的有2名选手的等级为优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)证明:k∈R,直线y=g(x)都不是曲线y=f(x)的切线;
(2)若x∈[e,e2],使得f(x)≤g(x)+ ![]() 成立,求实数k的取值范围.
成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司推广线下分店,计划在S市的A区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这x个分店的年收入之和.
x(个) | 2 | 3 | 4 | 5 | 6 |
y(百万元) | 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程 ![]() ;
;
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为z=y﹣0.05x2﹣1.4,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
(参考公式: ![]() ,其中
,其中  )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第五届北京农业嘉年华于2017年3月11日至5月7日在昌平区兴寿镇草莓博览园中举办,设置“三馆两园一带一谷一线”八大功能板块.现安排六名志愿者去其中的“三馆两园”参加志愿者服务工作,若每个“馆”与“园”都至少安排一人,则不同的安排方法种数为( )
A.C ![]() A
A ![]()
B.5C ![]() A
A ![]()
C.5A ![]()
D.C ![]() A
A ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若ax2+bx+c<0的解集为{x|x<-2,或x>4},则对于函数f(x)=ax2+bx+c应有( )
A.f(5)<f(2)<f(-1)
B.f(5)<f(-1)<f(2)
C.f(-1)<f(2)<f(5)
D.f(2)<f(-1)<f(5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com