练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数f（x）在R上可导，其导函数为f′（x），且函数y=（1﹣x）f′（x）的图象如图所示，则下列结论中一定成立的是（ ）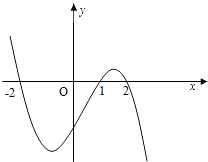

    A.函数f（x）有极大值f（2）和极小值f（1）
    B.函数f（x）有极大值f（﹣2）和极小值f（1）
    C.函数f（x）有极大值f（2）和极小值f（﹣2）
    D.函数f（x）有极大值f（﹣2）和极小值f（2）

    【答案】D
    【解析】解：由函数的图象可知，f′（﹣2）=0，f′（2）=0，并且当x＜﹣2时，f′（x）＞0，当﹣2＜x＜1，f′（x）＜0，函数f（x）有极大值f（﹣2）．
    又当1＜x＜2时，f′（x）＜0，当x＞2时，f′（x）＞0，故函数f（x）有极小值f（2）．
    故选D．
    利用函数的图象，判断导函数值为0时，左右两侧的导数的符号，即可判断极值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆C的极坐标方程为ρ=2cosθ，直线l的参数方程为 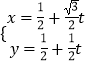（t为参数），点A的极坐标为（ ， ），设直线l与圆C交于点P、Q．
    （1）写出圆C的直角坐标方程；
    （2）求|AP||AQ|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数y=4x3+ax2+bx+5在x= 与x=﹣1时有极值．
    （1）写出函数的解析式；
    （2）指出函数的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，四棱锥的底面是梯形，且, 平面， 是中点， ．

    （Ⅰ）求证： 平面；

    （Ⅱ）若， ，求直线与平面所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}中，首项为a1（a1≠0），公差为d，前n项和为Sn ， 且满足a1S5+15=0，则实数d的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在锐角△ABC中，内角A，B，C的对边分别为a，b，c，且2asinB= b．
    （1）求角A的大小；
    （2）若a=6，b+c=8，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=ln（1+x），g（x）=xf′（x），x≥0，其中f′（x）是f（x）的导函数．
    （1）若f（x）≥ag（x）恒成立，求实数a的取值范围；
    （2）设n∈N* ， 证明： + +…+ ＜ln（n+1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆Γ： + =1（a＞b＞0）的右焦点与短轴两端点构成一个面积为2的等腰直角三角形，O为坐标原点：

    （1）求椭圆Г的方程：
    （2）设点A在椭圆Г上，点B在直线y=2上，且OA⊥OB，求证： + 为定值：
    （3）设点C在Γ上运动，OC⊥OD，且点O到直线CD距离为常数d（0＜d＜2），求动点D的轨迹方程：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为矩形，PA⊥平面ABCD，AB=PA=1，AD= ，F是PB中点，E为BC上一点．

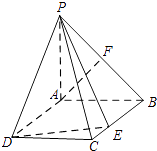
    （1）求证：AF⊥平面PBC；
    （2）当BE为何值时，二面角C﹣PE﹣D为45°．

    查看答案和解析>>

    同步练习册答案