
【题目】已知函数![]() (
(![]() ,
,![]() 是自然对数的底数)
是自然对数的底数)
(Ⅰ) 设![]() (其中
(其中![]() 是
是![]() 的导数),求
的导数),求![]() 的极小值;
的极小值;
(Ⅱ) 若对![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】
(Ⅰ)求出![]() ,分别令
,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间,结合单调性可求得函数的极值;(Ⅱ)由(Ⅰ)知,
的减区间,结合单调性可求得函数的极值;(Ⅱ)由(Ⅰ)知,![]() 在
在![]() 上单调递增,在(0,1)上单调递减,
上单调递增,在(0,1)上单调递减,![]() .讨论当
.讨论当![]() 时,当
时,当![]() 时两种情况,分别利用对数以及函数的单调性,求出函数最值,从而可筛选出符合题意的实数
时两种情况,分别利用对数以及函数的单调性,求出函数最值,从而可筛选出符合题意的实数![]() 的取值范围.
的取值范围.
(Ⅰ)![]() ,
,![]() .
.
令![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上为增函数,
上为增函数,![]() .
.
∵当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴![]() 的单调递减区间为(0,1),单调递增区间为
的单调递减区间为(0,1),单调递增区间为![]() ,
,
∴![]() .
.
(Ⅱ)由(Ⅰ)知,![]() 在
在![]() 上单调递增,在(0,1)上单调递减,
上单调递增,在(0,1)上单调递减,
∴![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,满足条件;
,满足条件;
当![]() 时,
时,![]() .
.
又∵![]() ,∴
,∴![]() ,使得
,使得![]() ,
,
此时,![]() ,
,![]() ;
;![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,![]() ,都有
,都有![]() ,不符合题意.
,不符合题意.
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,且
,且![]() 在椭圆
在椭圆![]() 上运动,当点
上运动,当点![]() 恰好在直线l:
恰好在直线l:![]() 上时,
上时,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)作与![]() 平行的直线
平行的直线![]() ,与椭圆交于
,与椭圆交于![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,若
,若![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( )
①已知函数![]() 是一次函数,若数列
是一次函数,若数列![]() 通项公式为
通项公式为![]() ,则该数列是等差数列;
,则该数列是等差数列;
②若直线![]() 上有两个不同的点到平面
上有两个不同的点到平面![]() 的距离相等,则
的距离相等,则![]() ;
;
③在![]() 中,“
中,“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
④若![]() ,则
,则![]() 的最大值为2.
的最大值为2.
A.1B.2C.3D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 件次品和
件次品和![]() 件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出
件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出![]() 件次品或者检测出
件次品或者检测出![]() 件正品时检测结束.
件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用![]() 元,设
元,设![]() 表示直到检测出
表示直到检测出![]() 件次品或者检测出
件次品或者检测出![]() 件正品时所需要的检测费用(单位:元),求
件正品时所需要的检测费用(单位:元),求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】惠州市某商店销售某海鲜,经理统计了春节前后50天该海鲜的日需求量![]() (
(![]() ,单位:公斤),其频率分布直方图如下图所示.该海鲜每天进货1次,每销售1公斤可获利40元;若供大于求,剩余的海鲜削价处理,削价处理的海鲜每公斤亏损10元;若供不应求,可从其它商店调拨,调拨的海鲜销售1公斤可获利30元.假设商店该海鲜每天的进货量为14公斤,商店销售该海鲜的日利润为
,单位:公斤),其频率分布直方图如下图所示.该海鲜每天进货1次,每销售1公斤可获利40元;若供大于求,剩余的海鲜削价处理,削价处理的海鲜每公斤亏损10元;若供不应求,可从其它商店调拨,调拨的海鲜销售1公斤可获利30元.假设商店该海鲜每天的进货量为14公斤,商店销售该海鲜的日利润为![]() 元.
元.
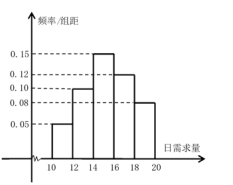
(1)求商店日利润![]() 关于日需求量
关于日需求量![]() 的函数表达式.
的函数表达式.
(2)根据频率分布直方图,
①估计这50天此商店该海鲜日需求量的平均数.
②假设用事件发生的频率估计概率,请估计日利润不少于620元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中,![]() 、
、![]() 分别在
分别在![]() 和
和![]() 上(异于端点),则过三点
上(异于端点),则过三点![]() 、
、![]() 、
、![]() 的平面被正方体截得的图形不可能是( )
的平面被正方体截得的图形不可能是( )
A.正方形B.不是正方形的菱形
C.不是正方形的矩形D.梯形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国正逐渐进入老龄化社会,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布被制作成如下图表:

据统计,该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发放生活补贴,标准如下:
①80岁及以上长者每人每月发放生活补贴300元;
②80岁以下老人每人每月发放生活补贴200元;
③不能自理的老人每人每月额外发放生活补贴100元.
则政府执行此计划的年度预算为 ___________万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com