
【题目】若正实数a,b满足a+b=1,则( )
A.![]() 有最大值4
有最大值4
B.ab有最小值 ![]()
C.![]() 有最大值
有最大值 ![]()
D.a2+b2有最小值 ![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为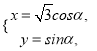 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线 ![]() 的两个焦点分别为F1、F2离心率e=2.
的两个焦点分别为F1、F2离心率e=2.
(1)求此双曲线的渐近线l1、l2的方程;
(2)若A、B分别为l1、l2上的点,且 ![]() 求线段AB的中点M的轨迹方程.
求线段AB的中点M的轨迹方程.
(3)过点N(1,0)能否作直线l , 使l与双曲线交于不同两点P、Q.且 ![]() ,若存在,求直线l的方程,若不存在,说明理由.
,若存在,求直线l的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,(a为常数且a>0).
,(a为常数且a>0).
(1)若函数的定义域为 ![]() ,值域为
,值域为 ![]() ,求a的值;
,求a的值;
(2)在(1)的条件下,定义区间(m,n),[m,n],(m,n],[m,n)的长度为n﹣m,其中n>m,若不等式f(x)+b>0,x∈[0,π]的解集构成的各区间的长度和超过 ![]() ,求b的取值范围.
,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{bn}是首项b1=1,b4=10的等差数列,设bn+2=3 ![]() an(n∈n*).
an(n∈n*).
(1)求证:{an}是等比数列;
(2)记cn= ![]() ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;
(3)记dn=(3n+1)Sn , 若对任意正整数n,不等式 ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() 恒成立,求整数m的最大值.
恒成立,求整数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|log0.5x|,若正实数m,n(m<n)满足f(m)=f(n),且f(x)在区间[m2 , n]上的最大值为4,则n﹣m=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1,2,3,4,现从盒子中随机抽取卡片.
(1)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于8的概率;
(2)若随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字3的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com