
【题目】某县共有90间农村淘宝服务站,随机抽取5间,统计元旦期间的网购金额(单位:万元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值;
(2)若网购金额(单位:万元)不小于18的服务站定义为优秀服务站,其余为非优秀服务站.根据茎叶图推断90间服务站中有几间优秀服务站?
(3)从随机抽取的5间服务站中再任取2间作网购商品的调查,求恰有1间是优秀服务站的概率.

科目:高中数学 来源: 题型:
【题目】某高三理科班共有60名同学参加某次考试,从中随机挑选出5名同学,他们的数学成绩![]() 与物理成绩
与物理成绩![]() 如下表:
如下表:
数学成绩 | 145 | 130 | 120 | 105 | 100 |
物理成绩 | 110 | 90 | 102 | 78 | 70 |
数据表明![]() 与
与![]() 之间有较强的线性关系.
之间有较强的线性关系.
(I)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(II)该班一名同学的数学成绩为110分,利用(I)中的回归方程,估计该同学的物理成绩;
(III)本次考试中,规定数学成绩达到125分为优秀,物理成绩达到100分为优秀. 若
该班数学优秀率与物理优秀率分别为50%和60%,且除去抽走的5名同学外,剩下的同学中数学优秀但物理不优秀的同学共有5人,在答卷页上填写下面2×2列联表,判断能否在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关?
物理优秀 | 物理不优秀 | 合计 | |
数学优秀 | |||
数学不优秀 | |||
合计 | 60 |
参考数据:回归直线的系数
![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入21世纪以来,南康区家具产业快速发展,为广大市民提供了数十万就业岗位,提高了广大市民的收入,也带动南康和周边县市的经济快速发展.同时,由于生产设备相对落后,生产过程中产生大量粉尘、废气,给人们的健康、交通安全等带来了严重影响.经研究发现,工业废气、粉尘等污染物排放是雾霾形成和持续的重要原因,治理污染刻不容缓.为此,某工厂新购置并安装了先进的废气、粉尘处理设备,使产生的废气、粉尘经过过滤后再排放,以降低对空气的污染.已知过滤过程中废气粉尘污染物的数量![]() (单位:
(单位:![]() )与过滤时间
)与过滤时间![]() (单位:
(单位:![]() )间的关系为
)间的关系为![]()
![]() (
(![]() 均为非零常数,
均为非零常数,![]() 为自然对数的底数)其中
为自然对数的底数)其中![]() 为
为![]() 时的污染物数量.若过滤
时的污染物数量.若过滤![]() 后还剩余
后还剩余![]() 的污染物.
的污染物.
(1)求常数![]() 的值.
的值.
(2)试计算污染物减少到![]() 至少需要多长时间(精确到
至少需要多长时间(精确到![]() .参考数据:
.参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为其右焦点,
为其右焦点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以 ![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直四棱柱![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 上的动点,且
上的动点,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
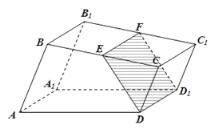
(1)证明:无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)当![]() 时,求几何体
时,求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若函数![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值;
的值;
(2)在(1)的结论下,若关于![]() 的不等式
的不等式![]() ,当
,当![]() 时恒成立,求
时恒成立,求![]() 的值;
的值;
(3)令![]() ,若关于
,若关于![]() 的方程
的方程![]() 在
在![]() 内至少有两个解,求出实数
内至少有两个解,求出实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用1个单位量的水可洗掉蔬菜上残留农药量的![]() ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用![]() 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数![]() .
.
(1)试规定![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(2)试根据假定写出函数![]() 应该满足的条件和具有的性质;
应该满足的条件和具有的性质;
(3)设![]() .现有
.现有![]() 单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较省?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较省?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com