
【题目】已知a>0,b>0,c>0,函数f(x)=|x﹣a|+|x+b|+c的最小值为1.
(1)求a+b+c的值;
(2)求证:a2+b2+c2 ![]() .
.
【答案】
(1)解:∵a>0,b>0,c>0,
∴f(x)=|x﹣a|+|x+b|+c≥|x﹣a﹣x﹣b|+c=a+b+c,
当且仅当(x﹣a)(x﹣b)≤0时:“=”成立,
故a+b+c=1
(2)证明:3(a2+b2+c2)﹣12
=3(a2+b2+c2)﹣(a+b+c)2
=2a2+2b2+2c2﹣2ab﹣2bc﹣2ac
=(a﹣b)2+(b﹣c)2+(c﹣a)2≥0,
∴a2+b2+c2 ![]()
【解析】(1)运用绝对值不等式的性质,注意等号成立的条件,即可求得最小值;(2)通过作差法证明即可.
【考点精析】通过灵活运用基本不等式,掌握基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
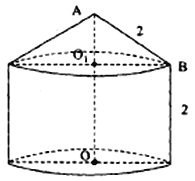
【题目】某粮库拟建一个储粮仓如图所示,其下部是高为2的圆柱,上部是母线长为2的圆锥,现要设计其底面半径和上部圆锥的高,若设圆锥的高![]() 为
为![]() ,储粮仓的体积为
,储粮仓的体积为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;(圆周率用
的函数关系式;(圆周率用![]() 表示)
表示)
(2)求![]() 为何值时,储粮仓的体积最大.
为何值时,储粮仓的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C对边分别为a,b,c,且c<a,已知 ![]() =﹣2,tanB=2
=﹣2,tanB=2 ![]() ,b=3.
,b=3.
(1)求a和c的值;
(2)求sin(B﹣C)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
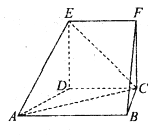
【题目】在如图所示的几何体中,四边形![]() 为正方形,四边形
为正方形,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() .
.
(1)求![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)线段![]() 或其延长线上是否存在点
或其延长线上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线相交于
与抛物线相交于![]() 两点,分别过点
两点,分别过点![]() 作抛物线的两条切线
作抛物线的两条切线![]() 和
和![]() ,记
,记![]() 和
和![]() 相交于点
相交于点![]() .
.
(1)证明:直线![]() 和
和![]() 的斜率之积为定值;
的斜率之积为定值;
(2)求证:点![]() 在一条定直线上.
在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|3≤![]() ≤27},B={x|
≤27},B={x|![]() >1}.
>1}.
(1)分别求A∩B,(![]() )∪A;
)∪A;
(2)已知集合C={x|1<x<a},若CA,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知⊙O的方程x2+y2=4,直线l:x=4,在以O为极点,x轴的正半轴为极轴的极坐标系中,过极点作射线交⊙O于A,交直线l于B.
(1)写出⊙O及直线l的极坐标方程;
(2)设AB中点为M,求动点M的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com