
【题目】已知函数f(x)=lnx+ ![]() (a>0).
(a>0).
(1)求函数f(x)在[1,+∞)上的最小值;
(2)若存在三个不同的实数xi(i=1,2,3)满足f(x)=ax.
(i)证明:a∈(0,1),f( ![]() )>
)> ![]() ;
;
(ii)求实数a的取值范围及x1x2x3的值.
【答案】
(1)解:函数f(x)的导数为f′(x)= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
当a≥1时,f(x)在[1,a]递减,在[a,+∞)递增,
可得f(x)在x=a取得极小值,且为最小值lna+1;
当0<a<1时,f′(x)>0,f(x)在[1,+∞)递增,
f(1)取得最小值,且为a.
综上可得当a≥1时,f(x)的最小值为lna+1;
当0<a<1时,f(x)的最小值为a;
(2)(i)证明:∵f(x)﹣ax=lnx﹣ax+ ![]() ,
,
∴f( ![]() )﹣
)﹣ ![]() =ln
=ln ![]() ﹣
﹣ ![]() +
+ ![]() =2lna﹣
=2lna﹣ ![]() +
+ ![]() ﹣ln2,
﹣ln2,
令g(a)=2lna﹣ ![]() +
+ ![]() ﹣ln2,
﹣ln2,
∴g′(a)= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴a∈(0,1)时,g'(a)<0,g(a)单调递减,
∴g(a)>g(1)=2﹣ ![]() ﹣ln2>0,
﹣ln2>0,
∴a∈(0,1),f( ![]() )>
)> ![]() ;
;
(ii)∵f(x)﹣ax的导数为f′(x)﹣a= ![]() ﹣a(1+
﹣a(1+ ![]() )=
)= ![]() ,
,
令f′(x)=a,∴﹣ax2+x﹣a=0,
∵函数f(x)﹣ax存在不同的零点,∴△=1﹣4a2>0,
解得﹣ ![]() <a<
<a< ![]() ,
,
由0<a< ![]() ,令f′(x)=a,得,x4=
,令f′(x)=a,得,x4= ![]() ,x5=
,x5= ![]() ,
,
此时,f(x)在(0,x4)上递减,(x4,x5)上递增,(x5,+∞)上递减,
∴f(x)至多有三个零点.
∵f(x)在(x4,1)递增,∴f(x4)<f(1)=a,
又∵f( ![]() )>
)> ![]() ,
,
∴x0∈( ![]() ,x4),使得f(x0)=a,
,x4),使得f(x0)=a,
又f( ![]() )=﹣f(x0)=a,f(1)=a,
)=﹣f(x0)=a,f(1)=a,
∴恰有三个不同零点:x0,1, ![]() ,
,
∴函数f(x)存在三个不同的零点时,a的取值范围是(0, ![]() );
);
且x1x2x3的值为1.
【解析】(1)求出f(x)的导数,对a讨论,当a≥1时,当0<a<1时,讨论单调区间,可得最小值;(2)(i)求出f( ![]() )﹣
)﹣ ![]() ,构造函数g(a)=2lna﹣
,构造函数g(a)=2lna﹣ ![]() +
+ ![]() ﹣ln2,利用导数求得g(a)>g(1)=2﹣
﹣ln2,利用导数求得g(a)>g(1)=2﹣ ![]() ﹣ln2>0,问题得以证明;(ii)求出原函数的导函数,然后讨论0<a<
﹣ln2>0,问题得以证明;(ii)求出原函数的导函数,然后讨论0<a< ![]() f(x)的零点的个数,即可得到x1x2x3的值.
f(x)的零点的个数,即可得到x1x2x3的值.


科目:高中数学 来源: 题型:
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: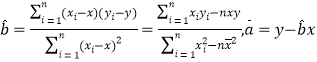 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2ωx﹣ ![]() )(ω>0)的最小正周期为4π,则( )
)(ω>0)的最小正周期为4π,则( )
A.函数f(x)的图象关于点( ![]() ,0)对称
,0)对称
B.函数f(x)的图象关于直线x= ![]() 对称
对称
C.函数f(x)的图象在( ![]() ,π)上单调递减
,π)上单调递减
D.函数f(x)的图象在( ![]() ,π)上单调递增
,π)上单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinxcosx+cos2x,x∈R.
sinxcosx+cos2x,x∈R.
(1)把函数f(x)的图象向右平移 ![]() 个单位,得到函数g(x)的图象,求g(x)在[0,
个单位,得到函数g(x)的图象,求g(x)在[0, ![]() ]上的最大值;
]上的最大值;
(2)在△ABC中,角A,B,C对应的三边分别为a,b,c,b= ![]() ,f(
,f( ![]() )=1,S△ABC=3
)=1,S△ABC=3 ![]() ,求a和c的值.
,求a和c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中学校在2015年的一次体能测试中,规定所有男生必须依次参加50米跑、立定跳远和一分钟的引体向上三项测试,只有三项测试全部达标才算合格,已知男生甲的50米跑和立定跳远的测试与男生乙的50米跑测试已达标,男生甲还需要参加一分钟的引体向上测试,男生乙还需要参加立定跳远和一分钟引体向上两项测试,若甲参加一分钟引体向上测试达标的概率为p,乙参加立定跳远和一分钟引体向上的测试达标的概率均为 ![]() ,甲乙每一项测试是否达标互不影响,已知甲和乙同时合格的概率为
,甲乙每一项测试是否达标互不影响,已知甲和乙同时合格的概率为 ![]() .
.
(1)求p的值,并计算甲和乙恰有一人合格的概率;
(2)在三项测试项目中,设甲达标的测试项目项数为x,乙达标的测试项目项数为y,记ξ=x+y,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三2班有48名学生进行了一场投篮测试,其中男生28人,女生20人.为了了解其投篮成绩,甲、乙两人分别对全班的学生进行编号(1~48号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮考试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
(Ⅰ)从甲抽取的样本数据中任取两名同学的投篮成绩,记“抽到投篮成绩优秀”的人数为X,求X的分布列和数学期望;
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
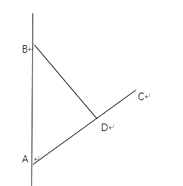
【题目】如图,准备在墙上钉一个支架,支架由两直杆AC与BD 焊接而成,焊接点 D 把杆AC 分成 AD, CD 两段,其中两固定点A,B 间距离为1 米,AB 与杆 AC 的夹角为60 ,杆AC 长为 1 米,若制作 AD 段的成本为a 元/米,制作 CD 段的成本是 2a 元/米,制作杆BD 成本是 3a 元/米. 设 ADB ,则制作整个支架的总成本记为 S 元.
(1)求S关于 的函数表达式,并求出的取值范围;
(2)问 ![]() 段多长时,S最小?
段多长时,S最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右顶点A(2,0),且过点
的右顶点A(2,0),且过点 ![]()
(1)求椭圆C的方程;
(2)过点B(1,0)且斜率为k1(k1≠0)的直线l于椭圆C相交于E,F两点,直线AE,AF分别交直线x=3于M,N两点,线段MN的中点为P,记直线PB的斜率为k2 , 求证:k1k2为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com