
【题目】若对于函数f(x)的定义域中任意的x1 , x2(x1≠x2),恒有 ![]() 和
和 ![]() 成立,则称函数f(x)为“单凸函数”,下列有四个函数:
成立,则称函数f(x)为“单凸函数”,下列有四个函数:
(1)y=2x;(2)y=lgx;(3) ![]() ;(4)y=x2 .
;(4)y=x2 .
其中是“单凸函数”的序号为 .
【答案】
(1)(2)(3)
【解析】解:根据题意,函数f(x)满足 ![]() 和
和 ![]() ,
,
则函数f(x)为增函数且图象向上凸起,
据此分析所给的4个函数:
对于(1)y=2x,函数为增函数但图象向下凹,不是“单凸函数”;
对于(2)y=lgx,函数f(x)为增函数且图象向上凸起,是“单凸函数”;
对于(3) ![]() ,函数f(x)为增函数且图象向上凸起,是“单凸函数”;
,函数f(x)为增函数且图象向上凸起,是“单凸函数”;
对于(4)y=x2,函数在其定义域不是增函数,不是“单凸函数”;
则(2)(3)是“单凸函数”;
所以答案是:(2)(3).
【考点精析】本题主要考查了函数的图象和函数单调性的判断方法的相关知识点,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值;单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若| ![]() ﹣
﹣ ![]() |=
|= ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() ;
;
(2)设c=(0,1),若 ![]() +
+ ![]() =c,求α,β的值.
=c,求α,β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() ,
, ![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ![]() =(﹣
=(﹣ ![]() ,1).
,1).
(1)若| ![]() |=2 且
|=2 且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标;
的坐标;
(2)若| ![]() |=
|= ![]() ,(
,( ![]() +3
+3 ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),求向量
),求向量 ![]() ,
, ![]() 的夹角的余弦值.
的夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF= ![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( ) 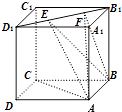
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A﹣BEF的体积为定值
D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1+x)﹣loga(1﹣x)(a>0且a≠1),
(1)求函数f(x)的定义域;
(2)若关于x的方程|f(x)|=2的解集为 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)判断f(x)的奇偶性;
(2)用单调性的定义证明f(x)为R上的增函数;
(3)若对任意的t∈R,不等式f(mt2+1)+f(1﹣mt)>0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,且an=2an﹣1+2n(n≥2,且n∈N*)
(1)求证:数列{ ![]() }是等差数列;
}是等差数列;
(2)求数列{an}的通项公式;
(3)设数列{an}的前n项之和Sn , 求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在奥运会射箭决赛中,参赛号码为1~4号的4名射箭运动员参加射箭比赛.
(1)通过抽签将他们安排到1~4号靶位,试求恰有2名运动员所抽靶位号与其参赛号码相同的概率;
(2)记1号、2号射箭运动员射箭的环数为ξ(ξ所有取值为0,1,2,3,…,10)分别为P1 , P2 . 根据教练员提供的资料,其概率分布如下表:
ξ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
P1 | 0 | 0 | 0 | 0 | 0.06 | 0.04 | 0.06 | 0.3 | 0.2 | 0.3 | 0.04 |
P2 | 0 | 0 | 0 | 0 | 0.04 | 0.05 | 0.05 | 0.2 | 0.32 | 0.32 | 0.02 |
①若1,2号运动员各射箭一次,求两人中至少有一人命中9环的概率;
②判断1号、2号射箭运动员谁射箭的水平高?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com