
【题目】下列几个命题
①奇函数的图象一定通过原点
②函数![]() 是偶函数,但不是奇函数
是偶函数,但不是奇函数
③函数f(x)=ax﹣1+3的图象一定过定点P,则P点的坐标是(1,4)
④若f(x+1)为偶函数,则有f(x+1)=f(﹣x﹣1)
⑤若函数 在R上的增函数,则实数a的取值范围为[4, 8)
在R上的增函数,则实数a的取值范围为[4, 8)
其中正确的命题序号为________.
【答案】③⑤
【解析】
①若在原点无意义,则奇函数图象就不过原点;②可整理为y=0,既为奇函数又为偶函数;③恒过的含义为无论参数a取何值,函数都过某一点;④利用偶函数的定义自变量x取相反数,函数值不变;⑤分段函数要使在整个区间单调,则必须每个区间都有相同的单调性,且在临界处满足单调性.
①奇函数的图象关于原点对称,若在原点有意义,则一定通过原点,故错误;
②函数![]() 的定义域为{﹣1,1},整理后y=0,即是偶函数,又是奇函数,故错误;
的定义域为{﹣1,1},整理后y=0,即是偶函数,又是奇函数,故错误;
③a0=1,当x=1时,f(1)=4,函数f(x)=ax﹣1+3的图象一定过定点P(1,4),故正确;
④若f(x+1)为偶函数,由偶函数定义可知f(﹣x+1)=f(x+1),故错误;
⑤若函数 在R上的增函数,
在R上的增函数,
∴a>1,且4﹣![]() >0,f(1)≤a,
>0,f(1)≤a,
∴实数a的取值范围为[4,8)故正确;
故正确答案为:为③⑤.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDE中,四边形ABED是直角梯形,∠BAD=90°,DE∥AB,△ACD是的正三角形,CD=AB=![]() DE=1,BC=
DE=1,BC=![]()
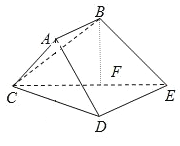
(1)求证:△CDE是直角三角形
(2) F是CE的中点,证明:BF⊥平面CDE
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为{x|x≠0}的函数f(x)满足:f(xy)=f(x)f(y),f(x)>0且在区间(0,+∞)上单调递增,若m满足f(log3m)+f( ![]() )≤2f(1),则实数m的取值范围是( )
)≤2f(1),则实数m的取值范围是( )
A.[ ![]() ,1)∪(1,3]
,1)∪(1,3]
B.[0, ![]() )∪(1,3]
)∪(1,3]
C.(0, ![]() ]
]
D.[1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个对应f,不是从集合A到集合B的函数的是( ).
A. A=![]() ,B={-6,-3,1},
,B={-6,-3,1},![]() ,f (1)=-3,
,f (1)=-3,![]() ;
;
B. A=B={x|x≥-1},f (x)=2x+1;
C. A=B={1,2,3},f (x)=2x-1;
D. A=Z,B={-1,1},n为奇数时,f (n)=-1,n为偶数时,f (n)=1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() .
.

(1)已画出函数![]() 在
在![]() 轴左侧的图像,如图所示,请补出完整函数
轴左侧的图像,如图所示,请补出完整函数![]() 的图像,并根据图像写出函数
的图像,并根据图像写出函数![]() 的增区间;
的增区间;
⑵写出函数![]() 的解析式和值域.
的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+bx(其中a,b为常数,a>0且a≠1,b>0且b≠1)的图象经过点A(1,6),![]() .
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若a>b,函数![]() ,求函数g(x)在[-1,2]上的值域.
,求函数g(x)在[-1,2]上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com