
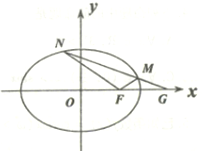
 已知椭圆$Ω:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,直线$\frac{{\sqrt{2}}}{2}x+y=1$经过Ω的右顶点和上顶点.
已知椭圆$Ω:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,直线$\frac{{\sqrt{2}}}{2}x+y=1$经过Ω的右顶点和上顶点.分析 (1)在方程$\frac{{\sqrt{2}}}{2}x+y=1$中,分别令x=0,y=0,可得a,b,即可得出.
(2)①设直线MN的方程为y=k(x-2)(k≠0).代入椭圆方程得(1+2k2)x2-8k2x+8k2-2=0.设M(x1,y1),N(x2,y2),利用斜率计算公式、一元二次方程的根与系数的关系即可证明.
②因为MN直线过点G(2,0),设直线MN的方程为y=k(x-2),即kx-y-2k=0代入椭圆方程得(1+2k2)x2-8k2x+8k2-2=0.由判别式△>0解得k范围.利用弦长公式、三角形面积计算公式、二次函数的单调性即可得出.
解答 解:(1)在方程$\frac{{\sqrt{2}}}{2}x+y=1$中,令x=0,则y=1,所以上顶点的坐标为(0,1),所以b=1;令y=0,则$x=\sqrt{2}$,所以右顶点的坐标为$({\sqrt{2},0})$,所以$a=\sqrt{2}$.
所以,椭圆Ω的方程为$\frac{x^2}{2}+{y^2}=1$.
(2)①设直线MN的方程为y=k(x-2)(k≠0).代入椭圆方程得(1+2k2)x2-8k2x+8k2-2=0.设M(x1,y1),N(x2,y2),则${x_1}+{x_2}=\frac{{8{k^2}}}{{1+2{k^2}}},{x_1}{x_2}=\frac{{8{k^2}-2}}{{1+2{k^2}}},{k_1}+{k_2}=\frac{y_1}{{{x_1}-1}}+\frac{y_2}{{{x_2}-1}}$=$\frac{{k({{x_1}-2})}}{{{x_1}-1}}+\frac{{k({{x_2}-2})}}{{{x_2}-1}}=k[{2-\frac{{{x_1}+{x_2}-2}}{{({{x_1}-1})({{x_2}-1})}}}]=k[{2-\frac{{\frac{{8{k^2}}}{{2{k^2}+1}}-2}}{{\frac{{8{k^2}-2}}{{2{k^2}+1}}-\frac{{8{k^2}}}{{2{k^2}+1}}+1}}}]=0$,
所以k1+k2=0,为定值.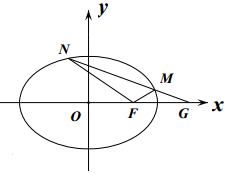
②因为MN直线过点G(2,0),设直线MN的方程为y=k(x-2),即kx-y-2k=0代入椭圆方程得(1+2k2)x2-8k2x+8k2-2=0.由判别式△=(-8k2)2-4(2k2+1)(8k2-2)>0解得${k^2}<\frac{1}{2}$.点F(1,0)到直线 MN的距离为h,则$h=\frac{{|{k-2k}|}}{{\sqrt{{k^2}+1}}}=\frac{|k|}{{\sqrt{{k^2}+1}}}.S=\frac{1}{2}|{MN}|•h=\frac{1}{2}\sqrt{{k^2}+1}•\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}•\frac{|k|}{{\sqrt{{k^2}+1}}}$=$\frac{1}{2}\sqrt{1+{k^2}}•\sqrt{\frac{{{{({8{k^2}})}^2}}}{{{{({2{k^2}+1})}^2}}}-4\frac{{8{k^2}-2}}{{2{k^2}+1}}}•\frac{|k|}{{\sqrt{{k^2}+1}}}$=$\frac{1}{2}|k|\frac{{\sqrt{8({1-2{k^2}})}}}{{2{k^2}+1}}=\sqrt{2}\sqrt{\frac{{({1-2{k^2}}){k^2}}}{{{{({2{k^2}+1})}^2}}}}$,令t=1+2k2,则$S=\sqrt{2}\sqrt{\frac{{-{t^2}+3t-2}}{{2{t^2}}}}=\sqrt{2}\sqrt{-{{({\frac{1}{t}-\frac{3}{4}})}^2}+\frac{1}{16}}$,所以${k^2}=\frac{1}{6}$时,S的最大值为$\frac{{\sqrt{2}}}{4}$.
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、弦长公式、三角形面积计算公式、二次函数的单调性、点到直线的距离公式,考查了推理能力与就你死了,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}V$ | B. | $\frac{1}{12}V$ | C. | $\frac{1}{16}V$ | D. | $\frac{1}{24}V$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l1⊥l2 | B. | l1∥l2 | ||
| C. | l1与l2相交不平行 | D. | l1与l2重合 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\frac{1}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{{\sqrt{10}}}{4}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com