
【题目】求证 :直角坐标平面上的格点凸七边形(每个顶点均为格点———纵 、横坐标均为整数的点)的内部最少包含四个格点.
【答案】见解析
【解析】
首先,不妨设格点凸七边形![]() 的各边的内部都没有格点(否则,如
的各边的内部都没有格点(否则,如![]() 的内部有一个格点
的内部有一个格点![]() ,则用七边形
,则用七边形![]() 代替原来的七边形,由于格点个数有限,故这种过程一定会在某一步终止).
代替原来的七边形,由于格点个数有限,故这种过程一定会在某一步终止).
其次,任何五个格点或五个顶点的坐标按奇偶性分类,至多有四类:(奇,奇),(偶,偶),(奇,偶),(偶,奇),因而,必有五个顶点中的某两个点属于同一类,这两点的中点![]() 也是格点,且点M在凸七边形的内部.
也是格点,且点M在凸七边形的内部.
考虑![]() 这五个格点,其中某两点的中点
这五个格点,其中某两点的中点![]() 也是格点,且点
也是格点,且点![]() 在七边形
在七边形![]() 的内部.
的内部.
同理,由格点五边形![]() (若
(若![]() 为
为![]() 的中点,则取格点五边形
的中点,则取格点五边形![]() )可确定另一个格点
)可确定另一个格点![]() 也在七边形
也在七边形![]() 的内部,如图所示.
的内部,如图所示.

直线![]() 将平面分为两部分,其中必有某一侧至少含有格点凸七边形的三个顶点.不妨设
将平面分为两部分,其中必有某一侧至少含有格点凸七边形的三个顶点.不妨设![]() 在
在![]() 的同一侧,则由凸五边形
的同一侧,则由凸五边形![]() 可知,七边形
可知,七边形![]() 的内部还有第三个格点
的内部还有第三个格点![]() .
.
(1)若![]() 的另一侧也含有七边形
的另一侧也含有七边形![]() 的三个顶点,同理可得第四个格点
的三个顶点,同理可得第四个格点![]() .
.
(2)若![]() 的另一侧至多含两个顶点
的另一侧至多含两个顶点![]() 和
和![]() ,则
,则![]() 、
、![]() 在直线
在直线![]() 上或与
上或与![]() 在
在![]() 的同一侧,这时,又有两种情况:
的同一侧,这时,又有两种情况:
(ⅰ)若点![]() 不在
不在![]() 内,则
内,则![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 组成凸五边形,又可得到一个格点(第四个)
组成凸五边形,又可得到一个格点(第四个)![]() ;
;
(ⅱ)若点![]() 在内(或边上),则
在内(或边上),则![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 组成凸(非凹)五边形,可得到第四个格点
组成凸(非凹)五边形,可得到第四个格点![]() (注:若
(注:若![]() 、
、![]() 在
在![]() 同一侧,
同一侧,![]() 、
、![]() 与
与![]() 、
、![]() 、
、![]() 在
在![]() 同侧,则考虑五边形
同侧,则考虑五边形![]() ).
).
另一方面,容易举出一个例子,使得七边形![]() 的内部恰有四个格点.
的内部恰有四个格点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若![]() 、
、![]() 均为非零整数,且
均为非零整数,且![]() 满足方程
满足方程![]() ,则称
,则称![]() 为方程的非零整数解.下列关于本方程非零整数解的判断中,为真命题的是( )
为方程的非零整数解.下列关于本方程非零整数解的判断中,为真命题的是( )
A. 非零整数解不存在
B. 存在有限个非零整数解
C. 存在无限个非零整数解,不在一、三象限
D. 存在无限个非零整数解,不在二、四象限
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一批草莓中,随机抽取![]() 个,其重量(单位:克)的频率分布表如下:
个,其重量(单位:克)的频率分布表如下:
分组(重量) |
|
|
|
|
频数(个) |
|
|
|
|
已知从![]() 个草莓中随机抽取一个,抽到重量在
个草莓中随机抽取一个,抽到重量在![]() 的草莓的概率为
的草莓的概率为![]() .
.
(1)求出![]() ,
,![]() 的值;
的值;
(2)用分层抽样的方法从重量在![]() 和
和![]() 的草莓中共抽取
的草莓中共抽取![]() 个,再从这
个,再从这![]() 个草莓中任取
个草莓中任取![]() 个,求重量在
个,求重量在![]() 和
和![]() 中各有
中各有![]() 个的概率.
个的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现代社会对破译密码的难度要求越来越高.有一种密码把英文的明文(真实文)按字母分解,其中英文的a,b,…,z这26个字母(不论大小写)依次对应1,2,…,26这26个自然表,见表
a | b | c | d | e | f | g | h | i | j | k | l | m |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
n | o | p | q | r | s | t | u | v | w | x | y | z |
14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
给出如下一个变换公式: 利用它可将明文转换成密文,如
利用它可将明文转换成密文,如![]() ,即h变成q;
,即h变成q;![]() ,即e变成c,按上述公式,若将某明文译成的密文是shxc,那么,原来的明文是( ).
,即e变成c,按上述公式,若将某明文译成的密文是shxc,那么,原来的明文是( ).
A. lhho B. ohhl C. love D. eovl
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个十进制正整数中,如果它含有偶数(包括零)个数字 8 ,则称它为“优数” ,否则就称它为“非优数” .那么,长度(位数)不超过![]() (
(![]() 是正整数)的所有“优数” 的个数是 __________.
是正整数)的所有“优数” 的个数是 __________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直角坐标系中曲线![]() 的参数方程:
的参数方程:![]() (
(![]() 为参数),在以坐标原点为极点,
为参数),在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,
轴正半轴为极轴的极坐标系中,![]() 点的极坐标
点的极坐标![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程;
的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知点
中,已知点![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 是曲线
是曲线![]() 上的任意一点,点
上的任意一点,点![]() 为
为![]() 的中点,以坐标原点为极点,
的中点,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求点![]() 的轨迹
的轨迹![]() 的极坐标方程;
的极坐标方程;
(2)已知直线![]() :
:![]() 与曲线
与曲线![]() 交于点
交于点![]() ,
,![]() ,射线
,射线![]() 逆时针旋转
逆时针旋转![]() 交曲线
交曲线![]() 于点
于点![]() ,且
,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点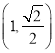 ,且两个焦点的坐标分别为
,且两个焦点的坐标分别为![]() ,
, ![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
, ![]() ,
, ![]() 为
为![]() 上的三个不同的点,
上的三个不同的点, ![]() 为坐标原点,且
为坐标原点,且![]() ,求证:四边形
,求证:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com