
已知函数
(1)写出函数 的单调区间;
的单调区间;
(2)若 在
在 恒成立,求实数
恒成立,求实数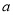 的取值范围;
的取值范围;
(3)若函数 在
在 上值域是
上值域是 ,求实数
,求实数 的取值范围.
的取值范围.
(1)增区间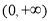 , 减区间
, 减区间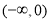 ;(2)实数
;(2)实数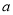 的取值范围为
的取值范围为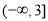
(3)实数 的取值范围为
的取值范围为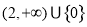
【解析】
试题分析:(1)由已知函数可化为 ,根据函数
,根据函数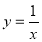 的单调区间,得出所求函数的单调区间;(2)由(1)可知不等式
的单调区间,得出所求函数的单调区间;(2)由(1)可知不等式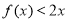 可化为
可化为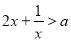 ,根据函数
,根据函数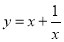 在
在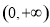 的单调性,可求得函数
的单调性,可求得函数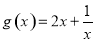 在
在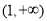 上的值域,从而求出所实数
上的值域,从而求出所实数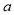 的范围;(3)由(1)可知函数
的范围;(3)由(1)可知函数 的单调区间,可将区间
的单调区间,可将区间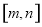 分
分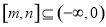 与
与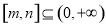 两种情况进行讨论,根据函数
两种情况进行讨论,根据函数 的单调性及值域,分别建立关于
的单调性及值域,分别建立关于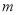 ,
,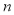 的方程组,由方程组解的情况,从而求出实数
的方程组,由方程组解的情况,从而求出实数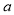 的取值范围.
的取值范围.
试题解析:(1)增区间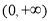 , 减区间
, 减区间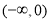 2分
2分
(2)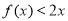 在
在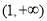 上恒成立即
上恒成立即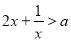 在
在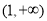 上恒成立
上恒成立
易证,函数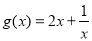 在
在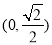 上递减,在
上递减,在 上递增
上递增
故当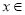
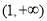 上有
上有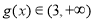
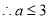
故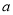 的取值范围为
的取值范围为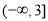 5分
5分
(3)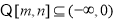 或
或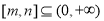
①当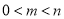 时,
时,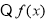 在
在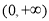 上递增,
上递增,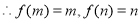
即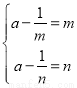 即方程
即方程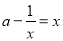 有两个不等正实数根
有两个不等正实数根
方程化为: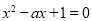 故
故 得
得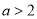 10分
10分
②当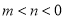 时
时
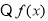 在
在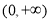 上递减
上递减 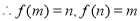
即 (1)-(2)得
(1)-(2)得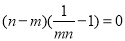
又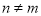 ,
,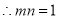
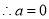 13分
13分
综合①②得实数 的取值范围为
的取值范围为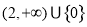 14分
14分
考点:1.分段函数;2.函数的单调性;3.分类讨论思想.


科目:高中数学 来源:2016届甘肃高台第一中学高一秋学期期末考试数学试卷(解析版) 题型:选择题
在用二分法求方程 的一个近似解时,现在已经将一根锁定在(1,2)内,则下一步可断定该根所在的区间为( )
的一个近似解时,现在已经将一根锁定在(1,2)内,则下一步可断定该根所在的区间为( )
A.(1.4,2) B.(1,1.4) C.(1,1.5) D.(1.5,2)
查看答案和解析>>
科目:高中数学 来源:2016届湖南张家界普通高中高一上学期期末联考数学卷(解析版) 题型:选择题
根据表格中的数据,可以断定方程 的一个根所在的区间是( )
的一个根所在的区间是( )
| -1 | 0 | 1 | 2 | 3 |
| 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| 1 | 2 | 3 | 4 | 5 |
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
查看答案和解析>>
科目:高中数学 来源:2016届湖北荆州中学高一上学期期中考试理科数学试卷(解析版) 题型:选择题
已知函数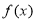 的定义域为
的定义域为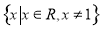 ,且
,且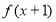 为奇函数,当
为奇函数,当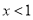 时,
时,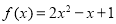 ,那么当
,那么当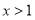 时,
时,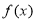 的递减区间是( )
的递减区间是( )
A.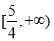 B.
B.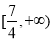 C.
C.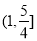 D.
D.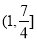
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com