Question

设函数f(x)的定义域为R，当x＜0时，f(x)＞1，且对任意的实数x,y∈R，有f(x+y)=f(x)·f(y)成立，数列{a_n}满足a₁=f(0)且f(a_n+1)=(n∈N^*)

(1)求a_{2 007}；

(2)若不等式(1+)(1+)…(1+)≥k·对一切n∈N^*均成立，求k的最大值.

Answer 1

解：(1)令x=-1,y=0,得f(-1)=f(-1)·f(0)f(0)=1.

∴a₁=f(0)=1，当x＞0时，-x＜0,f(-x)＞1,f(0)=f(x-x)=f(x)·f(-x)=1.

∴0＜f(x)＜1.

对任意x₁＜x₂,f(x₁)-f(x₂)=f(x₁)-f(x₁+x₂-x₁)=f(x₁)［1-f(x₂-x₁)］＞0,

∴f(x₁)＞f(x₂),∴f(x)为减函数,

由f(a_n+1)=,得f(a_n+1)·f(-2-a_n)=1,

故f(a_n+1-a_n-2)=f(0),∴a_n+1-a_n-2=0.

因此{a_n}是首项为1，公差为2的等差数列.

即a_n+1-a_n=2(n∈N^*),∴a_{2 007}=4 013.a_n=2n-1.                                        

(2)由(1+)(1+)…(1+)≥k·对一切n∈N^*恒成立，

知k≤恒成立.

设F(n)= 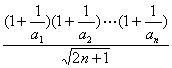,则F(n)＞0,

且F(n+1)=.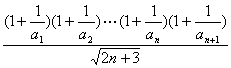

又＞1,

即F(n+1)＞F(n),故F(n)关于n为增函数,

∴F(n)≥F(1)=.∴k≤,∴k的最大值为.