
【题目】共享单车是指企业的校园,地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,某共享单车企业为更好服务社会,随机调查了100人,统计了这100人每日平均骑行共享单车的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知骑行时间在![]() 三组对应的人数依次成等差数列
三组对应的人数依次成等差数列
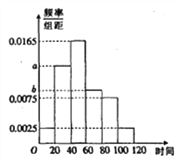
(1)求频率分布直方图中![]() 的值.
的值.
(2)若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”,将日平均骑行时间少于40分钟的用户为“潜力用户”,现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人,再从这5人中任取3人,求恰好1人为“忠实用户”的概率.
科目:高中数学 来源: 题型:
【题目】(导学号:05856290)[选修4-5:不等式选讲]
已知函数f(x)=|x-a|+|x-2a|.
(Ⅰ)对任意x∈R,不等式f(x)>1成立,求实数a的取值范围;
(Ⅱ)当a=-1时,解不等式f(x)<3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856301)已知函数f(x)=m(x-1)ex+![]() x2(m∈R),其导函数为f′(x),若对任意的x<0,不等式x2+(m+1)x>f′(x)恒成立,则实数m的取值范围为( )
x2(m∈R),其导函数为f′(x),若对任意的x<0,不等式x2+(m+1)x>f′(x)恒成立,则实数m的取值范围为( )
A. (0,1) B. (-∞,1) C. (-∞,1] D. (1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856333)
已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,其右焦点为F(c,0),第一象限的点A在椭圆C上,且AF⊥x轴.
,其右焦点为F(c,0),第一象限的点A在椭圆C上,且AF⊥x轴.
(Ⅰ)若椭圆C过点(1,- ![]() ),求椭圆C的标准方程;
),求椭圆C的标准方程;
(Ⅱ)已知直线l:y=x-c与椭圆C交于M,N两点,且B(4c,yB)为直线l上的点,证明:直线AM,AB,AN的斜率满足kAB=![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:“x0∈(-1,1),x-x0-m=0(m∈R)”是正确的,设实数m的取值集合为M.
(1)求集合M;
(2)设关于x的不等式(x-a)(x+a-2)<0(a∈R)的解集为N,若“x∈M”是“x∈N”的充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方体ABCD-A′B′C′D′的外接球的体积为![]() π,将正方体割去部分后,剩余几何体的三视图如图所示,则剩余几何体的表面积为( )
π,将正方体割去部分后,剩余几何体的三视图如图所示,则剩余几何体的表面积为( )
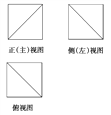
A. ![]() +
+![]() B. 3+
B. 3+![]() 或
或![]() +
+![]() C. 3+
C. 3+![]() D.
D. ![]() +
+![]() 或2+
或2+![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为了解辖区住户中离退休老人每天的平均户外“活动时间”,从辖区住户的离退休老人中随机抽取了100位老人进行调查,获得了每人每天的平均户外“活动时间”(单位:小时),活动时间按照![]() 、
、![]() 、…、
、…、![]() 从少到多分成9组,制成样本的频率分布直方图如图所示.
从少到多分成9组,制成样本的频率分布直方图如图所示.
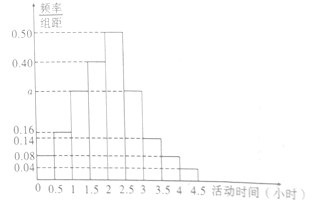
(1)求图中![]() 的值;
的值;
(2)估计该社区住户中离退休老人每天的平均户外“活动时间”的中位数;
(3)在![]() 、
、![]() 这两组中采用分层抽样抽取7人,再从这7人中随机抽取2人,求抽取的两人恰好都在同一个组的概率.
这两组中采用分层抽样抽取7人,再从这7人中随机抽取2人,求抽取的两人恰好都在同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 是大于0的常数).以坐标原点为极点,
是大于0的常数).以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的极坐标方程和圆
的极坐标方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)分别记直线![]() :
: ![]() ,
, ![]() 与圆
与圆![]() 、圆
、圆![]() 的异于原点的焦点为
的异于原点的焦点为![]() ,
, ![]() ,若圆
,若圆![]() 与圆
与圆![]() 外切,试求实数
外切,试求实数![]() 的值及线段
的值及线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com