
分析 (1)由an+1-an=2n,a1=1,利用an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1即可得出.
(2)由an+1-an=2n,a1=1.利用an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1,即可得出.
解答 解:(1)∵an+1-an=2n,a1=1,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2(n-1)+2(n-2)+…+2×1+1
=$2×\frac{n(n-1)}{2}$+1
=n2-n+1.
(2)∵an+1-an=2n,a1=1.
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2n-1+2n-2+…+2+1
=$\frac{{2}^{n}-1}{2-1}$
=2n-1.
点评 本题考查了“累加求和”、等差数列与等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:填空题
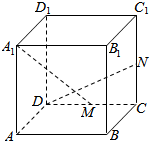 如图,在正方体ABCD-A1B1C1D1中,M,N分别是CD,CC1的中点,给出下列命题:
如图,在正方体ABCD-A1B1C1D1中,M,N分别是CD,CC1的中点,给出下列命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
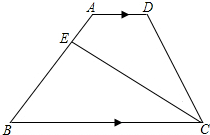 如图所示,在梯形ABCD中,BC∥AD,BC=3AD,点E在AB边上,且$\frac{AE}{BE}$=$\frac{1}{4}$,求△BEC的面积与四边形AECD的面积之比.
如图所示,在梯形ABCD中,BC∥AD,BC=3AD,点E在AB边上,且$\frac{AE}{BE}$=$\frac{1}{4}$,求△BEC的面积与四边形AECD的面积之比.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com