
【题目】从![]() 中任取
中任取![]() 个数,从
个数,从![]() 中任取
中任取![]() 个数,
个数,
(1)能组成多少个没有重复数字的四位数?
(2)若将(1)中所有个位是![]() 的四位数从小到大排成一列,则第
的四位数从小到大排成一列,则第![]() 个数是多少?
个数是多少?
【答案】(1) 1260 ;(2) 7205.
【解析】
(1)需要分两类:第一类,不选0时;第二类,选0时,根据分类计数原理可得;
(2)先分5种情况,形如①“1××5",②"2××5",③“3××5”,④“4××5”,⑤“6××5”,再寻找规律,问题得以解决.
解:(1)不选0时,有![]() 个;选0时,0不能排在首位,
个;选0时,0不能排在首位, ![]() ,根据分类计数原理,共有720+540=1260个四位数.
,根据分类计数原理,共有720+540=1260个四位数.
(2)①“1××5”,中间所缺的两数只能从0,2,4,6中选排,有![]() 个;
个;
②“2××5",中间所缺的两数是奇偶数各一个,有![]() 个;
个;
③“3××5",仿“1××5”,也有![]() 个;
个;
④“4××5",仿“2××5",也有![]() 个;
个;
⑤“6××5”也有![]() 个;
个;
即小于7000的数共有96个,故第97个数是7025,第98个数是7045,第99个数是7065,第100个数是7205.


科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数为______.
(1).设![]() 是一个区间,若对任意
是一个区间,若对任意![]() ,
,![]() ,当
,当![]() 时,都有
时,都有![]() ,则
,则![]() 在
在![]() 上单调递增;
上单调递增;
(2).函数![]() 在定义域上是单调递减函数;
在定义域上是单调递减函数;
(3).函数![]() 在定义域上是单调递增函数;
在定义域上是单调递增函数;
(4).集合![]() 与
与![]() 相等.
相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知![]() ,
, ![]() ,
,![]() ,D是边AC上的一点,将△ABC沿BD折叠,得到三棱锥A-BCD,若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设BM=x,则x的取值范围是( )
,D是边AC上的一点,将△ABC沿BD折叠,得到三棱锥A-BCD,若该三棱锥的顶点A在底面BCD的射影M在线段BC上,设BM=x,则x的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王投资1万元2万元、3万元获得的收益分别是4万元、9万元、16万元为了预测投资资金x(万元)与收益y万元)之间的关系,小王选择了甲模型![]() 和乙模型
和乙模型![]() .
.
(1)根据小王选择的甲、乙两个模型,求实数a,b,c,p,q,r的值
(2)若小王投资4万元,获得收益是25.2万元,请问选择哪个模型较好?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①某学校高二年级共有526人,为了调查学生每天用于休息的时间,决定抽取10%的学生进行调查;②运动会的工作人员为参加![]() 接力赛的6支队伍安排跑道;③一次数学月考中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人有解有关情况.针对这三个事件,恰当的抽样方法分别为( )
接力赛的6支队伍安排跑道;③一次数学月考中,某班有10人的成绩在100分以上,32人的成绩在90~100分,12人的成绩低于90分,现从中抽取9人有解有关情况.针对这三个事件,恰当的抽样方法分别为( )
A.分层抽样、分层抽样、简单随机抽样B.系统抽样、简单随机抽样、分层抽样
C.简单随机抽样、简单随机抽样、分层抽样D.系统抽样、分层抽样、简单随机抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数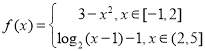 .
.
(1)在直角坐标系内直接画出![]() 的图象;
的图象;
(2)写出![]() 的单调区间,并指出单调性(不要求证明);
的单调区间,并指出单调性(不要求证明);
(3)若函数![]() 有两个不同的零点,求实数
有两个不同的零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
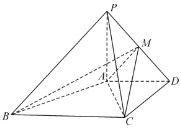
(1)求证:![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为45°,如果存在,求
的大小为45°,如果存在,求![]() 与平面
与平面![]() 所成角的正弦值,如果不存在,请说明理由.
所成角的正弦值,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com