Question

2．体积为$\frac{32π}{3}$的球有一个内接正三棱锥P-ABC，PQ是球的直径，∠APQ=60°，则三棱锥P-ABC的体积为（　　）

• A． $\frac{27\sqrt{3}}{4}$
• B． $\frac{9\sqrt{3}}{4}$
• C． $\frac{3\sqrt{3}}{4}$
• D． $\frac{\sqrt{3}}{4}$

Answer 1

分析 先确定球的半径，计算△ABC的面积，再计算三棱锥P一ABC的体积．

解答 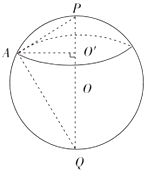解：由题意可得球O的半径为2，如图，
因为PQ是球的直径，所以∠PAQ=90°，∠APQ=60°，可得AP=2，
△ABC所在小圆圆心为O′，可由射影定理AP²=PO′•PQ，所以PO′=1，AO′=$\sqrt{3}$，
因为O′为△ABC的中心，所以可求出△ABC的边长为3，面积为$\frac{9\sqrt{3}}{4}$，
因此，三棱锥P-ABC的体积为V=$\frac{1}{3}×\frac{9\sqrt{3}}{4}×1$=$\frac{3\sqrt{3}}{4}$．
故选：C．

点评 本题考查球的内接正三棱锥，考查三棱锥体积的计算，正确计算△ABC的面积是关键．