分析:(1)先证明BE是异面直线AB与EB1的公垂线,再利用平面几何知识结合方程思想及解三角形的方法求出BE的长即可;
(2)过E作EG∥B1A1再证明∠AEG是二面角A-EB1-A1的平面角,利用平行证得∠AEG=∠BAE,只要求出tan∠BAE即得.
解答: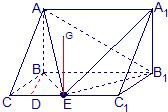
解:(Ⅰ)因AB⊥面BB
1C
1C,故AB⊥BE.
又EB
1⊥EA,且EA在面BCC
1B
1内的射影为EB.
由三垂线定理的逆定理知EB
1⊥BE,因此BE是异面直线AB与EB
1的公垂线,
在平行四边形BCC
1B
1中,设EB=x,则EB
1=
,
作BD⊥CC
1,交CC
1于D,则BD=BC•sin
=
.
在△BEB
1中,由面积关系得
x
=
•2•
,即(x
2-1)(x
2-3)=0.
解得x=±1,x=±
(负根舍去)
当x=
时,在△BCE中,CE
2+1
2-2CE•cos
=3,
解之得CE=2,故此时E与C
1重合,由题意舍去x=
.
因此x=1,即异面直线AB与EB
1的距离为1.
(Ⅱ)过E作EG∥B
1A
1,则GE⊥面BCC
1B,故GE⊥EB
1且GE在圆A
1B
1E内,
又已知AE⊥EB
1故∠AEG是二面角A-EB
1-A
1的平面角.
因EG∥B
1A
1∥BA,∠AEG=∠BAE,故tanAEG=
=
=
.
点评:本题主要考查了二面角及其度量,以及点、线、面间的距离计算,考查空间想象能力、运算能力和推理论证能力,属于基础题.

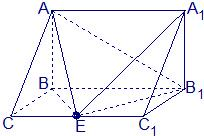 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB=
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB= 解:(Ⅰ)因AB⊥面BB1C1C,故AB⊥BE.
解:(Ⅰ)因AB⊥面BB1C1C,故AB⊥BE.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案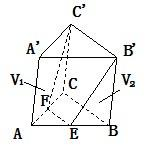 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )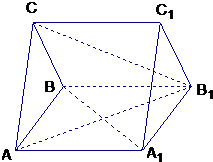 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2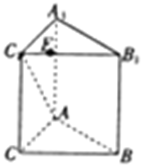 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.