
【题目】设函数![]() ,
,![]() 是定义域为R上的奇函数.
是定义域为R上的奇函数.
(1)求![]() 的值;
的值;
(2)已知![]() ,函数
,函数![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(3)若![]() ,试问是否存在正整数
,试问是否存在正整数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:
试题解析:(1)先利用![]() 为
为![]() 上的奇函数得
上的奇函数得![]() 求出以
求出以![]() 及函数
及函数![]() 的表达式,(2)先由
的表达式,(2)先由![]() 得
得![]() ,得出函数
,得出函数![]() 的单调性,再对
的单调性,再对![]() 进行整理,整理为用
进行整理,整理为用![]() 表示的函数,最后利用函数
表示的函数,最后利用函数![]() 的单调性以及值域,得到
的单调性以及值域,得到![]() 的值域.
的值域.
(3)利用换元法,将不等式转化为对勾函数问题求解,注意分类讨论思想的应用.
试题解析:(1)![]() 是定义域为R上的奇函数,
是定义域为R上的奇函数, ![]() ,得
,得![]() .
.
(2)![]() ,即
,即![]() ,
,![]() 或
或![]() (舍去),
(舍去),
![]()
令![]() ,由(1)知
,由(1)知![]() 在[1,2]上为增函数,∴
在[1,2]上为增函数,∴![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 有最大值
有最大值![]() ;当
;当![]() 时,
时,![]() 有最小值
有最小值![]() ,
,
∴![]() 的值域
的值域![]() .
.
(3)![]() =
=![]() ,
,![]() ,
,
假设存在满足条件的正整数![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() .
.
②当![]() 时,
时,![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,易证
,易证![]() 在
在![]() 上是增函数,∴
上是增函数,∴![]() .
.
③当![]() 时,
时,![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,易证
,易证![]() 在
在![]() 上是减函数,∴
上是减函数,∴![]() .
.
综上所述,![]() ,∵
,∵![]() 是正整数,∴
是正整数,∴![]() =3或4.
=3或4.
∴存在正整数![]() =3或4,使得
=3或4,使得![]() 对
对![]() 恒成立.
恒成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对某个品牌的U盘进行寿命追踪调查,所得情况如下面频率分布直方图所示. 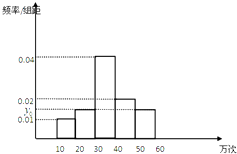
(1)图中纵坐标y0处刻度不清,根据图表所提供的数据还原y0;
(2)根据图表的数据按分层抽样,抽取20个U盘,寿命为1030万次之间的应抽取几个;
(3)从(2)中抽出的寿命落在1030万次之间的元件中任取2个元件,求事件“恰好有一个寿命为1020万次,一个寿命为2030万次”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的二项展开式中所有奇数项的系数之和为512,
的二项展开式中所有奇数项的系数之和为512,
(1)求展开式的所有有理项(指数为整数).
(2)求(1﹣x)3+(1﹣x)4+…+(1﹣x)n展开式中x2项的系数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M是R的子集,如果点x0∈R满足:a>0,x∈M,0<|x﹣x0|<a,称x0为集合M的聚点.则下列集合中以1为聚点的有( ) ① ![]() ;
;
② ![]() ;
;
③Z;
④{y|y=2x}.
A.①④
B.②③
C.①②
D.①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三边长为a,b,c,则下列命题中真命题是( )
A.“a2+b2>c2”是“△ABC为锐角三角形”的充要条件
B.“a2+b2<c2”是“△ABC为钝角三角形”的必要不充分条件
C.“a3+b3=c3”是“△ABC为锐角三角形”的既不充分也不必要条件
D.“ ![]() +
+ ![]() =
= ![]() ”是“△ABC为钝角三角形”的充分不必要条件
”是“△ABC为钝角三角形”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有各色球12只,其中5个红球,4个黑球,2个白球,1个绿球;从中随机取出1球.求:
(1)取出的1球是红球或黑球的概率;
(2)取出的1球是红球或黑球或白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com