
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)若![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)记t=lnx+x,通过讨论a的范围,结合函数的单调性以及函数的零点的个数判断a的范围即可.
(1)定义域为:![]() ,
,
当![]() 时,
时,![]() .
.
∴![]() 在
在![]() 时为减函数;在
时为减函数;在![]() 时为增函数.
时为增函数.
(2)记![]() ,则
,则![]() 在
在![]() 上单增,且
上单增,且![]() .∴
.∴![]()
![]() .∴
.∴![]() 在
在![]() 上有两个零点等价于
上有两个零点等价于![]() 在
在![]() 上有两个零点.
上有两个零点.
①在![]() 时,
时,![]() 在
在![]() 上单增,且
上单增,且![]() ,故
,故![]() 无零点;②在
无零点;②在![]() 时,
时,![]() 在
在![]() 上单增,又
上单增,又![]() ,
,![]() ,故
,故![]() 在
在![]() 上只有一个零点;
上只有一个零点;
③在![]() 时,由
时,由![]() 可知
可知![]() 在
在![]() 时有唯一的一个极小值
时有唯一的一个极小值![]() .
.
若![]() ,
,![]() ,
,![]() 无零点;若
无零点;若![]() ,
,![]() ,
,![]() 只有一个零点;若
只有一个零点;若![]() 时,
时,![]() ,而
,而![]() ,由于
,由于![]() 在
在![]() 时为减函数,可知:
时为减函数,可知:![]() 时,
时,![]() .从而
.从而![]() ,∴
,∴![]() 在
在![]() 和
和![]() 上各有一个零点.综上讨论可知:
上各有一个零点.综上讨论可知:![]() 时
时![]() 有两个零点,即所求
有两个零点,即所求![]() 的取值范围是
的取值范围是![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
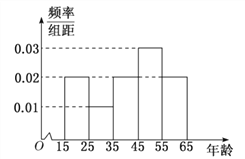
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15![]() 65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | /td> | ||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年![]() 月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在
月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在![]() 岁之间的
岁之间的![]() 人进行调查,经统计“年轻人”与“中老年人”的人数之比为
人进行调查,经统计“年轻人”与“中老年人”的人数之比为![]() .
.
关注 | 不关注 | 合计 | |
年轻人 |
| ||
中老年人 | |||
合计 |
|
|
|
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
(2)现已用分层抽样的办法从中老年人中选取了![]() 人进行问卷调查.若再从这
人进行问卷调查.若再从这![]() 人中选取
人中选取![]() 人进行面对面询问,求事件“选取的
人进行面对面询问,求事件“选取的![]() 人中恰有
人中恰有![]() 人关注“中国湖北(潜江)龙虾节””的概率.
人关注“中国湖北(潜江)龙虾节””的概率.
附:参考公式![]() ,其中
,其中![]() .
.
临界值表:
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解全市统考情况,从所有参加考试的考生中抽取4000名考生的成绩,频率分布直方图如下图所示.

(1)求这4000名考生的半均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由直方图可认为考生考试成绩z服从正态分布![]() ,其中
,其中![]() 分别取考生的平均成绩
分别取考生的平均成绩![]() 和考生成绩的方差
和考生成绩的方差![]() ,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
(3)如果用抽取的考生成绩的情况来估计全市考生的成绩情况,现从全市考生中随机抽取4名考生,记成绩不超过84.81分的考生人数为![]() ,求
,求![]() .(精确到0.001)
.(精确到0.001)
附:①![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为制定合理的节电方案,对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:百度),将数据按照![]() ,
,![]() ,
,![]() 分成
分成![]() 组,制成了如图所示的频率分布直方图:
组,制成了如图所示的频率分布直方图:

(I)求直方图中![]() 的值;
的值;
56789月均用电量百厦
(Ⅱ)设该市有100万户居民,估计全市每户居民中月均用电量不低于6百度的人数,估计每户居民月均用电量的中位数,说明理由;
(Ⅲ)政府计划对月均用电量在4(百度)以下的用户进行奖励,月均用电量在![]() 内的用户奖励20元/月,月均用电量在
内的用户奖励20元/月,月均用电量在![]() 内的用户奖励10元/月,月均用电量在
内的用户奖励10元/月,月均用电量在![]() 内的用户奖励2元/月.若该市共有400万户居民,试估计政府执行此计划的年度预算.
内的用户奖励2元/月.若该市共有400万户居民,试估计政府执行此计划的年度预算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线![]() 的焦点,离心率等于
的焦点,离心率等于![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右焦点
的右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,求证
,求证![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“吸烟有害健康,吸烟会对身体造成伤害”,哈尔滨市于2012年5月31日规定室内场所禁止吸烟.美国癌症协会研究表明,开始吸烟年龄X分别为16岁、18岁、20岁和22岁者,其得肺癌的相对危险度Y依次为15.10,12.81,9.72,3.21;每天吸烟支数U分别为10,20,30者,其得肺癌的相对危险度V分别为7.5,9.5和16.6,用![]() 表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
A.r1=r2B.r1>r2>0
C.0<r1<r2D.r1<0<r2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某公司2001年至2017年新产品研发费用![]() (单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了
(单位:万元)的折线图.为了预测该公司2019年的新产品研发费用,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据2001年至2017年的数据(时间变量
的两个线性回归模型.根据2001年至2017年的数据(时间变量![]() 的值依次为1,2,…,17)建立模型①:
的值依次为1,2,…,17)建立模型①:![]() ;根据2011年至2017年的数据(时间变量
;根据2011年至2017年的数据(时间变量![]() 的值依次为1,2,…,7)建立模型②:
的值依次为1,2,…,7)建立模型②:![]() .
.

(1)分别利用这两个模型,求该公司2019年的新产品研发费用的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com