
【题目】已知圆![]() 过定点
过定点![]() ,圆心
,圆心![]() 在抛物线
在抛物线![]() 上,
上,![]() 、
、![]() 为圆
为圆![]() 与
与![]() 轴的交点.
轴的交点.
(1)求圆![]() 半径的最小值;
半径的最小值;
(2)当圆心![]() 在抛物线上运动时,
在抛物线上运动时,![]() 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心![]() 在抛物线上运动时,记
在抛物线上运动时,记![]() ,
,![]() ,求
,求![]() 的最大值,并求此时圆的方程.
的最大值,并求此时圆的方程.
【答案】(1)![]() ;(2)
;(2)![]() ,证明见解析;(3)
,证明见解析;(3)![]() ,
,![]()
【解析】
(1)设半径为![]() ,根据抛物线方程设出圆心坐标,然后根据圆心和定点写出半径
,根据抛物线方程设出圆心坐标,然后根据圆心和定点写出半径![]() 的表达式,计算
的表达式,计算![]() 的最小值即可;
的最小值即可;
(2)根据(1)中的![]() 表示,写出圆的方程,令
表示,写出圆的方程,令![]() 计算出
计算出![]() 的横坐标,计算
的横坐标,计算![]() 是否为定值即可证明;
是否为定值即可证明;
(3)计算出![]() 的值,然后利用已求的值对
的值,然后利用已求的值对![]() 进行化简,再根据基本不等式确定最大值,从而求出圆心坐标和半径确定出圆的方程.
进行化简,再根据基本不等式确定最大值,从而求出圆心坐标和半径确定出圆的方程.
(1)设圆心坐标为![]() ,半径为
,半径为![]() ,所以
,所以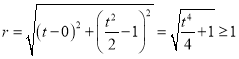 ,取等号时
,取等号时![]() ,所以
,所以![]() ;
;
(2)因为圆心坐标为![]() ,半径
,半径 ,所以圆的方程为:
,所以圆的方程为: ,
,
令![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 为定值
为定值![]() ;
;
(3)由(2)可知:取![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以
 ,
,
所以![]() 的最大值为
的最大值为![]() ,
,
取等号时![]() ,所以
,所以![]() ,所以圆心坐标为
,所以圆心坐标为![]() ,半径
,半径![]() ,
,
所以圆的方程为:![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知曲线![]() 上的动点
上的动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离相等.
的距离相等.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 分别作射线
分别作射线![]() 、
、![]() 交曲线
交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() ,且以
,且以![]() 为直径的圆经过点
为直径的圆经过点![]() .试探究直线
.试探究直线![]() 是否过定点?如果是,请求出该定点;如果不是,请说明理由.
是否过定点?如果是,请求出该定点;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是一块边长为7米的正方形铁皮,其中
是一块边长为7米的正方形铁皮,其中![]() 是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮
是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮![]() ,其中P是
,其中P是![]() 上一点.设
上一点.设![]() ,长方形
,长方形![]() 的面积为S平方米.
的面积为S平方米.

(1)求S关于![]() 的函数解析式;
的函数解析式;
(2)设![]() ,求S关于t的表达式以及S的最大值.
,求S关于t的表达式以及S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个无穷数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() 、
、![]() ,
,![]() ,
,![]() ,对任意的
,对任意的![]() ,都有
,都有![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 为等差数列,对任意的
为等差数列,对任意的![]() ,都有
,都有![]() ,证明:
,证明:![]() ;
;
(3)若![]() 为等比数列,
为等比数列,![]() ,
,![]() ,求满足
,求满足![]() (
(![]() )的
)的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,若数列
,若数列![]() 的各项按如下规律排列:
的各项按如下规律排列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() , …,
, …,![]() ,…有如下运算和结论:①
,…有如下运算和结论:①![]() ;②数列
;②数列![]() ,
,![]() ,
,![]() ,
,![]() ,…是等比数列;③数列
,…是等比数列;③数列![]() ,
,![]() ,
,![]() ,
,![]() ,…的前
,…的前![]() 项和为
项和为![]() ;④若存在正整数
;④若存在正整数![]() ,使
,使![]() ,
,![]() ,则
,则![]() .其中正确的结论是_____.(将你认为正确的结论序号都填上)
.其中正确的结论是_____.(将你认为正确的结论序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AB是圆O的直径,C,D是圆上不同两点,且![]() ,
,![]() ,
,![]() 圆O所在平面.
圆O所在平面.
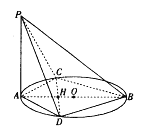
(1)求直线PB与CD所成角;
(2)若PB与圆O所在平面所成角为![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电动车售后服务调研小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.

(1)求续驶里程在![]() 的车辆数;
的车辆数;
(2)求续驶里程的平均数;
(3)若从续驶里程在![]() 的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在
的车辆中随机抽取2辆车,求其中恰有一辆车的续驶里程在![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com