(本题满分12分)设函数
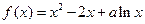
。
???(1)若函数

是定义域上的单调函数,求实数
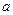
的取值范围;
???(2)求函数

的极值点。
1)
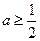
(2)
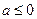
时,

在
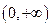
上有唯一的极小值点
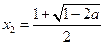
;
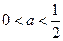
时,

有一个极大值点
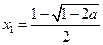
和一个极小值点
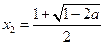
;
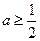
时,函数

在
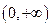
上无极值点。
1)
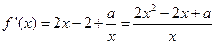
,若函数

是定义域上的单调函数,则只能
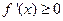
在
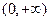
上恒成立,即
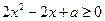
在
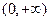
上恒成立恒成立,令
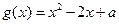
,则函数
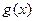
图象的对称轴方程是
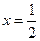
,故只要
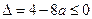
恒成立,即只要
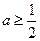
。(5分)
(2)有(1)知当
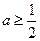
时,
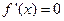
的点是导数不变号的点,
故
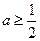
时,函数无极值点;
当
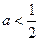
时,
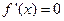
的根是
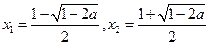
,
若
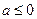
,
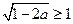
,此时
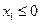
,
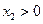
,且在
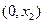
上
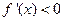
,
在
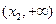
上
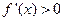
,故函数

有唯一的极小值点
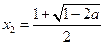
;(7分)
当
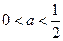
时,
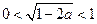
,此时
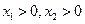
,
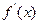
在
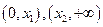
都大于
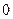
,
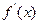
在
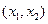
上小于
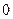
,
此时

有一个极大值点
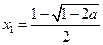
和一个极小值点
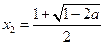
.(11分)
综上可知,
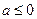
时,

在
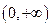
上有唯一的极小值点
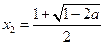
;
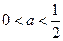
时,

有一个极大值点
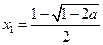
和一个极小值点
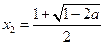
;
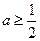
时,函数

在
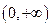
上无极值点。(12分)
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
设函数
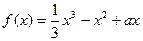
,
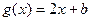
,当
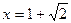
时,
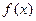
取得极值;
(1) 求
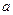
的值,并判断
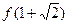
是函数
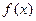
的极大值还是极小值;
(2) 当
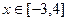
时,函数
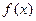
与
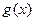
的图象有两个公共点,求
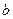
的取值范围;
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)
已知函数
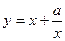
有如下性质:如果常数
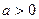
,那么该函数在
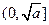
上是减函数,
在
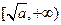
上是增函数,


(Ⅰ)如果函数
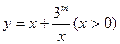
的值域是
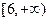
,求实数
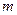
的值;
(Ⅱ)研究函数
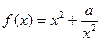
(常数
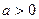
)在定义域内的单调性,并说明理由;
(Ⅲ)若把函数
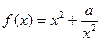
(常数
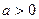
)在[1,2]上的最小值记为
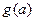
,
求
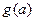
的表达式

查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
曲线
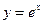
在点
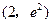
处的切线与坐标轴所围三角形的面积为 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
与曲线
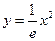
相切于
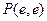
处的切线方程是(其中
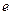
是自然对数的底)( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
过曲线
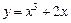
上一点
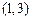
的切线方程是
▲ .
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知两曲线
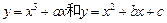
都经过点P(1,2),且在点P处有公切线,则当
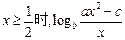
的最小值为( )
| A.-1 | B.1 | C.2 | D.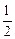 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知函数
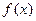
在R上满足
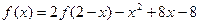
,则曲线
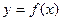
在点
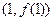
处的切线方程是( )
查看答案和解析>>

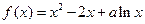 。
。 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数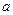 的取值范围;
的取值范围; 的极值点。
的极值点。 阅读快车系列答案
阅读快车系列答案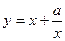 有如下性质:如果常数
有如下性质:如果常数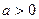 ,那么该函数在
,那么该函数在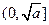 上是减函数,
上是减函数,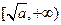 上是增函数,
上是增函数,

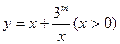 的值域是
的值域是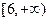 ,求实数
,求实数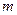 的值;
的值;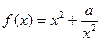 (常数
(常数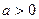 )在定义域内的单调性,并说明理由;
)在定义域内的单调性,并说明理由;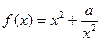 (常数
(常数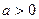 )在[1,2]上的最小值记为
)在[1,2]上的最小值记为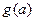 ,
,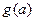 的表达式
的表达式