练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一扇形的周长为20cm，当扇形的圆心角α等于多少时，这个扇形的面积最大？最大面积是多少？

    【答案】解：设扇形的半径为r，弧长为l，则
    l+2r=20，即l=20﹣2r（0＜r＜10）．
    扇形的面积S= lr，将上式代入，
    得S= （20﹣2r）r=﹣r2+10r=﹣（r﹣5）2+25，
    所以当且仅当r=5时，S有最大值25，
    此时l=20﹣2×5=10，
    可得：α= =2rad．
    所以当α=2rad时，扇形的面积取最大值，最大值为25cm2 ．
    【解析】设扇形的半径为r，弧长为l，利用周长关系，表示出扇形的面积，利用二次函数求出面积的最大值，以及圆心角的大小．
    【考点精析】认真审题，首先需要了解扇形面积公式(若扇形的圆心角为，半径为，弧长为，周长为，面积为，则，，)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知命题p：x∈A，且A={x|a﹣1＜x＜a+1}，命题q：x∈B，且B={x|x2﹣4x+3≥0}
    （Ⅰ）若A∩B=，A∪B=R，求实数a的值；
    （Ⅱ）若p是q的充分条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在y=2x2上有一点P，它到A（1，3）的距离与它到焦点的距离之和最小，则点P的坐标是（ ）
    A.（﹣2，1）
    B.（1，2）
    C.（2，1）
    D.（﹣1，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为1，P、Q分别为边AB、DA上的点，当△APQ的周长为2时，求∠PCQ的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 .

    （1）若 ，求曲线 在点 处的切线方程；

    （2）若对任意 在恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在梯形中， ， ， ，四边形为矩形，平面平面， .

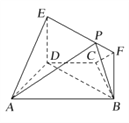
    （Ⅰ）求证： 平面；

    （Ⅱ）点在线段上运动，设平面与平面所成锐二面角为，试求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于平面向量，有下列四个命题：
    ①若 ．
    ② =（1，1）， =（2，x），若 与 平行，则x=2．
    ③非零向量 和 满足| |=| |=| |，则 与 的夹角为60°．
    ④点A（1，3），B（4，﹣1），与向量 同方向的单位向量为（ ）．
    其中真命题的序号为 ． （写出所有真命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校从高一年级A，B两个班中各选出7名学生参加物理竞赛，他们的成绩（单位：分）的茎叶图如图所示，其中A班学生的平均分是85分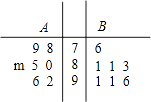

    （1）求m的值，并计算A班7名学生成绩的方差s2；
    （2）从成绩在90分以上的学生中随机抽取两名学生，求至少有一名A班学生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若数据x1 ， x2 ， x3 ， x4 ， x5的方差为3，则数据2x1+1，2x2+1，2x3+1，2x4+1，2x5+1的方差为 ．

    查看答案和解析>>

    同步练习册答案