
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,且
,且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明:![]() .
.
【答案】(1)-1;(2)![]() ;(3)参考解析
;(3)参考解析
【解析】
试题(1)![]() ,可知
,可知![]() 在[
在[![]() ,1]是增函数,在[1,2]是减函数,所以最大值为f(1).(2)
,1]是增函数,在[1,2]是减函数,所以最大值为f(1).(2)![]() 在区间
在区间![]() 上为单调递增函数,即
上为单调递增函数,即![]() 在
在![]() 上恒成立。
上恒成立。![]() ,利用分离参数
,利用分离参数![]() 在
在![]() 上恒成立,即求
上恒成立,即求![]() 的最大值。
的最大值。
(3)![]() 有两个实根
有两个实根![]() ,
, ![]() ,两式相减
,两式相减![]() ,又
,又![]() ,
,![]()
![]() .要证:
.要证:![]() ,只需证:
,只需证:![]() ,令
,令![]() 可证。
可证。
试题解析:(1) ![]()
函数![]() 在[
在[![]() ,1]是增函数,在[1,2]是减函数,
,1]是增函数,在[1,2]是减函数,
所以![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
因为![]() 在区间
在区间![]() 单调递增函数,所以
单调递增函数,所以![]() 在(0,3)恒成立
在(0,3)恒成立
![]() ,有
,有![]() =
=![]() ,(
,(![]() )
)
综上:![]()
(3)∵![]() ,又
,又![]() 有两个实根
有两个实根![]() ,
,
∴![]() ,两式相减,得
,两式相减,得![]() ,
,
∴![]() ,
,
于是![]()
![]() .
.
![]()
要证:![]() ,只需证:
,只需证:![]()
只需证:![]() .(*)
.(*)
令![]() ,∴(*)化为
,∴(*)化为 ![]() ,只证
,只证![]() 即可.
即可.
![]() 在(0,1)上单调递增,
在(0,1)上单调递增,![]() ,
,
即![]() .∴
.∴![]() .
.
(其他解法根据情况酌情给分)


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】图甲中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律、对捕食者和被捕食者数量之间的关系描述错误的是( )
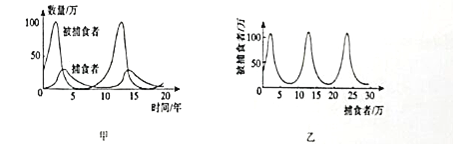
A. 捕食者和被捕食者数量与时间以![]() 年为周期
年为周期
B. 由图可知,当捕食者数量增多的过程中,被捕食者数量先增多后减少
C. 捕食者和被捕食者数量之间的关系可以用图1乙描述
D. 捕食者的数量在第![]() 年和
年和![]() 年之间数量在急速减少
年之间数量在急速减少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对![]() 名六年级学生进行了问卷调查,得到如下列联表(平均每天喝
名六年级学生进行了问卷调查,得到如下列联表(平均每天喝![]() 以上为常喝,体重超过
以上为常喝,体重超过![]() 为肥胖):
为肥胖):
常喝 | 不常喝 | 合计 | |
肥胖 |
|
|
|
不胖 |
|
|
|
合计 |
|
|
|
(1)已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,求抽到肥胖的学生的概率?
人,求抽到肥胖的学生的概率?
(2)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)现从常喝碳酸饮料且肥胖的学生中(其中![]() 名女生),抽取
名女生),抽取![]() 人参加电视节目,则正好抽到一男一女的概率是多少?
人参加电视节目,则正好抽到一男一女的概率是多少?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在微信群中发了一个8元“拼手气”红包,被甲、乙、丙三人抢完,若三人均领到整数元,且每人至少领到1元,则甲领到的钱数不少于其他任何人的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为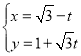 (t为参数),曲线C的极坐标方程为ρ=4sin(θ+
(t为参数),曲线C的极坐标方程为ρ=4sin(θ+![]() ).
).
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,求△MON的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】信息科技的进步和互联网商业模式的兴起,全方位地改变了大家金融消费的习惯和金融交易模式,现在银行的大部分业务都可以通过智能终端设备完成,多家银行职员人数在悄然减少.某银行现有职员320人,平均每人每年可创利20万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.2万元,但银行需付下岗职员每人每年6万元的生活费,并且该银行正常运转所需人数不得小于现有职员的![]() ,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com