
【题目】函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,周期是
,周期是![]() .
.
(1)求函数解析式,并写出函数图象的对称轴方程和对称中心;
(2)已知点![]() ,点
,点![]() 是该函数图象上一点,点
是该函数图象上一点,点![]() 是
是![]() 的中点,当
的中点,当![]() ,
, ![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)根据周期是![]() 可得
可得![]() 的值,再由图象与
的值,再由图象与![]() 轴交于点
轴交于点![]() 求得
求得![]() 的值,从而可得函数解析式,根据余弦函数的性质可求得函数
的值,从而可得函数解析式,根据余弦函数的性质可求得函数![]() 图象的对称轴方程和对称中心;(2)点
图象的对称轴方程和对称中心;(2)点![]()
![]() 是
是![]() 的中点,点
的中点,点![]() ,利用中点坐标公式求出
,利用中点坐标公式求出![]() 的坐标,点
的坐标,点![]() 是该函数图象上一点,代入函数解析式,化简,根据
是该函数图象上一点,代入函数解析式,化简,根据![]() ,求解
,求解![]() 的值.
的值.
试题解析:(1)由题意,周期是π,即![]() .
.
由图象与y轴交于点(0,![]() ),∴
),∴![]() ,可得
,可得![]() ,
,
∵0≤φ≤![]() ,
,![]()
得函数解析式![]() .
.
由![]() ,可得对称轴方程为
,可得对称轴方程为![]() ,(k∈Z)
,(k∈Z)
由![]() ,可得对称中心坐标为(
,可得对称中心坐标为(![]() ,0),(k∈Z)
,0),(k∈Z)
(2)![]() 点Q
点Q![]() 是PA的中点, A
是PA的中点, A![]() ,∴P的坐标为
,∴P的坐标为![]() ,
,
由![]() ,可得P的坐标为
,可得P的坐标为![]() ,
,
又∵点P是该函数图象上一点,
∴![]() ,
,
整理可得:![]() ,
,
∵x0∈![]() ,∴
,∴![]() ,
,
故![]() 或
或![]() ,
,
解得![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
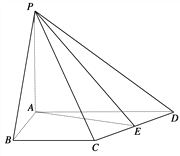
(1)证明:CD⊥平面PAE;
(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据报道,某公司的32名职工的月工资(单位:元)如下:
职务 | 董事长 | 副董事长 | 董事 | 总经理 | 经理 | 管理 | 职员 |
人数 | 1 | 1 | 2 | 1 | 5 | 3 | 20 |
工资 | 5 500 | 5 000 | 3 500 | 3 000 | 2 500 | 2 000 | 1 500 |
(1)求该公司职工工资的平均数、中位数、众数.(精确到1元)
(2)假设副董事长的工资从5 000元提升到20 000元,董事长的工资从5 500元提升到30 000元,那么新的平均数、中位数、众数分别是多少?(精确到1元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平?结合此问题谈一谈你的看法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世界卫生组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
某试点城市环保局从该市市区2016年全年每天的PM2.5监测数据中随机抽取6天的数据作为样本,监测值茎叶图(十位为茎,个位为叶)如图所示,若从这6天的数据中随机抽出2天,

(1)求恰有一天空气质量超标的概率;
(2)求至多有一天空气质量超标的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的![]() 倍.
倍.

(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1: ![]() ,(t为参数)曲线C2:
,(t为参数)曲线C2: ![]() +y2=4.
+y2=4.
(1)在同一平面直角坐标系中,将曲线C2上的点按坐标变换y′=yx,后得到曲线C′.求曲线C′的普通方程,并写出它的参数方程;
(2)若C1上的点P对应的参数为t= ![]() ,Q为C′上的动点,求PQ中点M到直线C3:
,Q为C′上的动点,求PQ中点M到直线C3: ![]() (t为参数)的距离的最小值.
(t为参数)的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络的发展,人们可以在网络上购物、玩游戏、聊天、导航等,所以人们对上网流量的需求越来越大.某电信运营商推出一款新的“流量包”套餐.为了调查不同年龄的人是否愿意选择此款“流量包”套餐,随机抽取50个用户,按年龄分组进行访谈,统计结果如表.
组号 | 年龄 | 访谈人数 | 愿意使用 |
1 | [18,28) | 4 | 4 |
2 | [28,38) | 9 | 9 |
3 | [38,48) | 16 | 15 |
4 | [48,58) | 15 | 12 |
5 | [58,68) | 6 | 2 |
(Ⅰ)若在第2、3、4组愿意选择此款“流量包”套餐的人中,用分层抽样的方法抽取12人,则各组应分别抽取多少人?
(Ⅱ)若从第5组的被调查者访谈人中随机选取2人进行追踪调查,求2人中至少有1人愿意选择此款“流量包”套餐的概率.
(Ⅲ)按以上统计数据填写下面2×2列联表,并判断以48岁为分界点,能否在犯错误不超过1%的前提下认为,是否愿意选择此款“流量包”套餐与人的年龄有关?
年龄不低于48岁的人数 | 年龄低于48岁的人数 | 合计 | |
愿意使用的人数 | |||
不愿意使用的人数 | |||
合计 |
参考公式: ![]() ,其中:n=a+b+c+d.
,其中:n=a+b+c+d.
P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等式:sin25°+cos235°+sin5°cos35°= ![]() ; sin215°+cos245°+sin15°cos45°=
; sin215°+cos245°+sin15°cos45°= ![]() ; sin230°+cos260°+sin30°cos60°=
; sin230°+cos260°+sin30°cos60°= ![]() ;由此可归纳出对任意角度θ都成立的一个等式,并予以证明.
;由此可归纳出对任意角度θ都成立的一个等式,并予以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为 ![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ![]() ,
, ![]() ,
, ![]() ,且各人回答正确与否相互之间没有影响,用ξ表示乙队的总得分. (Ⅰ)求ξ的分布列和数学期望;
,且各人回答正确与否相互之间没有影响,用ξ表示乙队的总得分. (Ⅰ)求ξ的分布列和数学期望;
(Ⅱ)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com