
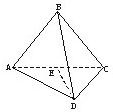
 解:如图,作BE⊥AC于E,
解:如图,作BE⊥AC于E,| 12 |
| 5 |
| 9 |
| 5 |
| 81 |
| 25 |
| 9 |
| 5 |
| 4 |
| 5 |
| 193 |
| 25 |
| ||
| 5 |


科目:高中数学 来源:2013届广西北海市合浦县教育局教研室高二下期中数学试卷(解析版) 题型:解答题
把长、宽各为4、3的长方形ABCD沿对角线AC折成直二面角,求顶点B和D的距离。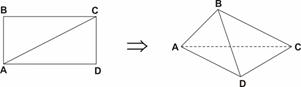
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:9.13 立体几何的综合问题(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com