
【题目】如图,圆![]() :
:![]() .
.

(Ⅰ)若圆C与x轴相切,求圆C的方程;
(Ⅱ)已知![]() ,圆
,圆![]() 与x轴相交于两点
与x轴相交于两点![]() (点
(点![]() 在点
在点![]() 的左侧).过点
的左侧).过点![]() 任作一条直线与圆
任作一条直线与圆![]() :
:![]() 相交于两点A,B.问:是否存在实数a,使得
相交于两点A,B.问:是否存在实数a,使得![]() =
=![]() ?若存在,求出实数a的值,若不存在,请说明理由.
?若存在,求出实数a的值,若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】已知O为![]() 内一点,若分别满足①
内一点,若分别满足①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() (其中
(其中![]() 为
为![]() 中,角
中,角![]() 所对的边).则O依次是
所对的边).则O依次是![]() 的( )
的( )
A.内心、重心、垂心、外心B.外心、垂心、重心、内心
C.外心、内心、重心、垂心D.内心、垂心、外心、重心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子的繁殖问题时,发现有这样的一列数:1,1,2,3,5,8,…,该数列的特点是:前两个数均为1,从第三个数起,每一个数都等于它前面两个数的和.人们把这样的一列数组成的数列![]() 称为斐波那契数列. 并将数列
称为斐波那契数列. 并将数列![]() 中的各项除以4所得余数按原顺序构成的数列记为
中的各项除以4所得余数按原顺序构成的数列记为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
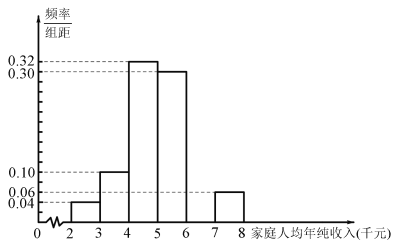
【题目】某贫困地区截至2018年底,按照农村家庭人均年纯收入8000元的小康标准,该地区仅剩部分家庭尚未实现小康.现从这些尚未实现小康的家庭中随机抽取50户,得到这50户家庭2018年的家庭人均年纯收入的频率分布直方图.
(1)补全频率分布直方图,并求出这50户家庭人均年纯收入的中位数和平均数(精确到元);
(2)2019年7月,为估计该地能否在2020年全面实现小康,统计了该地当时最贫困的一个家庭2019年1至6月的人均月纯收入如表:
月份/2019(时间代码 | 1 | 2 | 3 | 4 | 5 | 6 |
人居月纯收入 (元) | 275 | 365 | 415 | 450 | 470 | 485 |
由散点图及相关性分析发现:家庭人均月纯收入![]() 与时间代码
与时间代码![]() 之间具有较强的线性相关关系,请求出回归直线方程;并由此估计该家庭2020年1月的家庭人均月纯收入.
之间具有较强的线性相关关系,请求出回归直线方程;并由此估计该家庭2020年1月的家庭人均月纯收入.
①可能用到的数据:![]() ;
;
②参考公式:线性回归方程![]() 中,
中,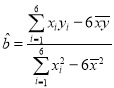 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
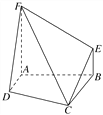
【题目】如图,四边形ABEF和四边形ABCD均是直角梯形,∠FAB=∠DAB=90°,二面角FABD是直二面角,BE∥AF,BC∥AD,AF=AB=BC=2,AD=1.
(1)证明:在平面BCE上,一定存在过点C的直线l与直线DF平行;
(2)求二面角FCDA的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电力公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行综合排序,综合排序高者中标。分值权重表如下:
总分 | 技术 | 商务 | 报价 |
100% | 50% | 10% | 40% |
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的。报价表则相对灵活,报价标的评分方法是:基准价的基准分是68分,若报价每高于基准价1%,则在基准分的基础上扣0.8分,最低得分48分;若报价每低于基准价1%,则在基准分的基础上加0.8分,最高得分为80分。若报价低于基准价15%以上(不含15%)每再低1%,在80分在基础上扣0.8分。在某次招标中,若基准价为1000(万元)。甲、乙两公司综合得分如下表:
公司 | 技术 | 商务 | 报价 |
甲 | 80分 | 90分 |
|
乙 | 70分 | 100分 |
|
甲公司报价为1100(万元),乙公司的报价为800(万元)则甲,乙公司的综合得分,分别是
A. 73,75.4 B. 73,80 C. 74.6,76 D. 74.6 ,75.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】意大利数学家列昂纳多·斐波那契是第一个研究了印度和阿拉伯数学理论的欧洲人,斐波那契数列被誉为是最美的数列,斐波那契数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB是圆O的直径,C是圆O上一点,AC=BC,且PA⊥平面ABC,E是AC的中点,F是PB的中点,PA=![]() ,AB=2.求:
,AB=2.求:
(Ⅰ)异面直线EF与BC所成的角;
(Ⅱ)点A到平面PBC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中装有除颜色外其他均相同的编号为a,b的两个黑球和编号为c,d,e的三个红球,从中任意摸出两个球.
(1)求恰好摸出1个黑球和1个红球的概率:
(2)求至少摸出1个黑球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com