
【题目】甲、乙两人各射击一次,击中目标的概率分别是 ![]() 和
和 ![]() .假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?
【答案】
(1)解:记“甲连续射击4次,至少1次未击中目标”为事件A1,
由题意知两人射击是否击中目标,相互之间没有影响,
射击4次,相当于4次独立重复试验,
故P(A1)=1﹣P( ![]() )=1﹣
)=1﹣ ![]() =
= ![]() .
.
即甲射击4次,至少1次未击中目标的概率为 ![]()
(2)解:记“甲射击4次,恰好击中目标2次”为事件A2,
“乙射击4次,恰好击中目标3次”为事件B2,
P(A2)= ![]() =
= ![]() ,
,
P(B2)= ![]() =
= ![]() .
.
由于甲、乙设计相互独立,
故P(A2B2)=P(A2)P(B2)= ![]()
![]() =
= ![]() .
.
即两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率为 ![]()
(3)解:记“乙恰好射击5次后,被中止射击”为事件A3,
“乙第i次射击为击中”为事件Di,(i=1,2,3,4,5),
则A3=D5D4 ![]() (
( ![]() ),且P(Di)=
),且P(Di)= ![]() ,
,
由于各事件相互独立,
故P(A3)=P(D5)P(D4)P( ![]() )P(
)P( ![]() )=
)= ![]() ×
× ![]() ×
× ![]() ×(1﹣
×(1﹣ ![]() ×
× ![]() )=
)= ![]() ,
,
即乙恰好射击5次后,被中止射击的概率是 ![]()
【解析】(1)由题意知,两人射击是否击中目标,相互之间没有影响;击中目标的概率分别是 ![]() 和
和 ![]() ,射击4次,相当于4次独立重复试验,根据独立重复试验和互斥事件的概率公式得到结果.(2)两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次,表示相互独立的两个事件同时发生,写出两个事件的概率,根据相互独立事件的概率公式得到结果.(3)乙恰好射击5次后,被中止射击,表示最后两次射击一定没有射中,前两次最多一次没击中,这几个事件之间是相互独立的,根据相互独立事件同时发生的概率得到结果.
,射击4次,相当于4次独立重复试验,根据独立重复试验和互斥事件的概率公式得到结果.(2)两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次,表示相互独立的两个事件同时发生,写出两个事件的概率,根据相互独立事件的概率公式得到结果.(3)乙恰好射击5次后,被中止射击,表示最后两次射击一定没有射中,前两次最多一次没击中,这几个事件之间是相互独立的,根据相互独立事件同时发生的概率得到结果.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC所在的平面内,点P0、P满足 ![]() =
= ![]()
![]() ,
, ![]() ,且对于任意实数λ,恒有
,且对于任意实数λ,恒有 ![]()
![]() ,则( )
,则( )
A.∠ABC=90°
B.∠BAC=90°
C.AC=BC
D.AB=AC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数f(x)与第x天近似地满足f(x)=8+ ![]() (千人),且参观民俗文化村的游客人均消费g(x)近似地满足g(x)=143﹣|x﹣22|(元).
(千人),且参观民俗文化村的游客人均消费g(x)近似地满足g(x)=143﹣|x﹣22|(元).
(1)求该村的第x天的旅游收入p(x)(单位千元,1≤x≤30,x∈N*)的函数关系;
(2)若以最低日收入的20%作为每一天纯收入的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术搏物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标总是中随机抽取3个总题,已知这6个招标问题中,甲公司可正确回答其中4道题目,而乙公司能正面回答每道题目的概率均为 ![]() ,甲、乙两家公司对每题的回答都是相独立,互不影响的.
,甲、乙两家公司对每题的回答都是相独立,互不影响的.
(1)求甲、乙两家公司共答对2道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是双曲线
是双曲线 ![]() 的右焦点,过点
的右焦点,过点 ![]() 作
作 ![]() 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为 ![]() ,线段
,线段 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,记点
,记点 ![]() 到
到 ![]() 的两条渐近线的距离之积为
的两条渐近线的距离之积为 ![]() ,若
,若 ![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A.![]()
B.2
C. 3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣3)2+(y﹣4)2=4,直线l过定点A(1,0).
(1)若l与圆C相切,求l的方程;
(2)若l与圆C相交于P、Q两点,若|PQ|=2 ![]() ,求此时直线l的方程.
,求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象与函数h(x)=x+ ![]() +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求f(x)的解析式;
(2)若g(x)=f(x)x+ax,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4 ![]() ,AD=2
,AD=2 ![]() ,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.
,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.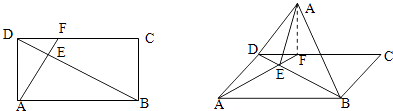
(1)当θ=90°时,求A′C的长;
(2)当cosθ= ![]() 时,求BC与平面A′BD所成角的正弦值.
时,求BC与平面A′BD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com