
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)求出函数![]() 的导数,分
的导数,分![]() 和
和![]() 两种情况讨论,分析导数
两种情况讨论,分析导数![]() 的符号变化,即可求出函数
的符号变化,即可求出函数![]() 的单调区间;
的单调区间;
(2)问题变形为![]() ,令
,令![]() ,由题意得出
,由题意得出![]() ,根据函数
,根据函数![]() 的单调性确定
的单调性确定![]() 的范围即可.
的范围即可.
(1)![]() ,定义域为
,定义域为![]() 且
且![]() .
.
①当![]() 时,则
时,则![]() ,则函数
,则函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,由
时,由![]() ,得
,得![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
此时,函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() .
.
综上所述,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ;
;
(2)![]() 变形为
变形为![]() ,
,
令![]() ,定义域为
,定义域为![]() ,且
,且![]() ,
,
![]() .
.
①当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,函数
,函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,
此时,![]() ,合乎题意;
,合乎题意;
②当![]() 时,则函数
时,则函数![]() 在
在![]() 上的单调减区间为
上的单调减区间为![]() ,单调增区间为
,单调增区间为![]() .
.
(i)当![]() 时,即当
时,即当![]() 时,则函数
时,则函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,
此时![]() ,则函数
,则函数![]() 在区间
在区间![]() 上为增函数.
上为增函数.
此时,![]() ,合乎题意;
,合乎题意;
(ii)当![]() 时,即当
时,即当![]() 时,则函数
时,则函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,所以,
上单调递增,所以,![]() ,
,
又![]() ,所以,函数
,所以,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,不合乎题意.
,不合乎题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆上的点到右焦点
,椭圆上的点到右焦点![]() 的距离的最大值为3.
的距离的最大值为3.
(1)求椭圆![]() 的方程;
的方程;
(2)若过椭圆![]() 的右焦点
的右焦点![]() 作倾斜角不为零的直线
作倾斜角不为零的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,设线段
,设线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了引导居民合理用水,居民生活用水实行二级阶梯式水价计量方法,具体如下;第一阶梯,每户居民每月用水量不超过12吨,价格为4元/吨;第二阶梯,每户居民用水量超过12吨,超过部分的价格为8元/吨,为了了解全是居民月用水量的分布情况,通过抽样获得了100户居民的月用水量(单位:吨),将数据按照![]() (全市居民月用水量均不超过16吨)分成8组,制成了如图1所示的频率分布直方图.
(全市居民月用水量均不超过16吨)分成8组,制成了如图1所示的频率分布直方图.
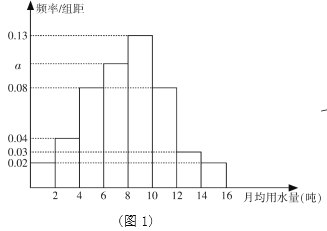
(Ⅰ)求频率分布直方图中字母![]() 的值,并求该组的频率;
的值,并求该组的频率;
(Ⅱ)通过频率分布直方图,估计该市居民每月的用水量的中位数![]() 的值(保留两位小数);
的值(保留两位小数);
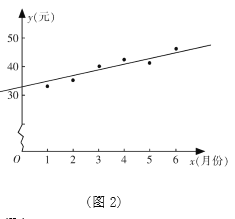
(Ⅲ)如图2是该市居民张某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() 若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .三角形
.三角形![]() 的两条边
的两条边![]() ,
,![]() 所在直线的斜率之积是
所在直线的斜率之积是![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,点
,点![]() ,
,![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将所有平面向量组成的集合记作![]() ,
,![]() 是从
是从![]() 到
到![]() 的对应关系,记作
的对应关系,记作![]() 或
或![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() 都是实数,定义对应关系
都是实数,定义对应关系![]() 的模为:在
的模为:在![]() 的条件下
的条件下![]() 的最大值记作
的最大值记作![]() ,若存在非零向量
,若存在非零向量![]() ,及实数
,及实数![]() 使得
使得![]() ,则称
,则称![]() 为
为![]() 的一个特殊值;
的一个特殊值;
(1)若![]() ,求
,求![]() ;
;
(2)如果![]() ,计算
,计算![]() 的特征值,并求相应的
的特征值,并求相应的![]() ;
;
(3)若![]() ,要使
,要使![]() 有唯一的特征值,实数
有唯一的特征值,实数![]() 、
、![]() 、
、![]() 、
、![]() 应满足什么条件?试找出一个对应关系
应满足什么条件?试找出一个对应关系![]() ,同时满足以下两个条件:①有唯一的特征值
,同时满足以下两个条件:①有唯一的特征值![]() ,②
,②![]() ,并验证
,并验证![]() 满足这两个条件.
满足这两个条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李克强总理在2018年政府工作报告指出,要加快建设创新型国家,把握世界新一轮科技革命和产业变革大势,深入实施创新驱动发展战略,不断增强经济创新力和竞争力.某手机生产企业积极响应政府号召,大力研发新产品,争创世界名牌.为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
单价 |
|
|
|
|
|
|
销量 |
|
|
|
|
|
|
已知![]() .
.
(1)若变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(2)用(1)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() .当销售数据
.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从
称为一个“好数据”.现从![]() 个销售数据中任取
个销售数据中任取![]() 个子,求“好数据”个数
个子,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式:线性回归方程中![]() 的估计值分别为
的估计值分别为 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com