(1)解:当n=1时,有a
13=a
12,
由于a
n>0,所以a
1=1.
当n=2时,有a
13+a
23=(a
1+a
2)
2,
将a
1=1代入上式,由于a
n>0,所以a
2=2.
(2)解:由于a
13+a
23++a
n3=(a
1+a
2++a
n)
2,①
则有a
13+a
23++a
n3+a
n+13=(a
1+a
2++a
n+a
n+1)
2.②
②-①,得a
n+13=(a
1+a
2++a
n+a
n+1)
2-(a
1+a
2++a
n)
2,
由于a
n>0,所以a
n+12=2(a
1+a
2++a
n)+a
n+1.③
同样有a
n2=2(a
1+a
2++a
n-1)+a
n(n≥2),④
③-④,得a
n+12-a
n2=a
n+1+a
n.
所以a
n+1-a
n=1.
由于a
2-a
1=1,即当n≥1时都有a
n+1-a
n=1,所以数列{a
n}是首项为1,公差为1的等差数列.
故a
n=n.
(3)解:由(2)知a
n=n,则

.
所以
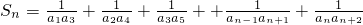
=
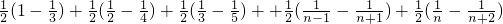
=

=
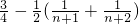
.
∵
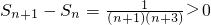
,
∴数列{S
n}单调递增.
所以
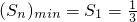
.
要使不等式
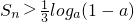
对任意正整数n恒成立,只要
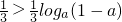
.
∵1-a>0,∴0<a<1.
∴1-a>a,即

.
所以,实数a的取值范围是

.
分析:(1)由题设条件知a
1=1.当n=2时,有a
13+a
23=(a
1+a
2)
2,由此可知a
2=2.
(2)由题意知,a
n+13=(a
1+a
2++a
n+a
n+1)
2-(a
1+a
2++a
n)
2,由于a
n>0,所以a
n+12=2(a
1+a
2++a
n)+a
n+1.同样有a
n2=2(a
1+a
2++a
n-1)+a
n(n≥2),由此得a
n+12-a
n2=a
n+1+a
n.所以a
n+1-a
n=1.所以数列{a
n}是首项为1,公差为1的等差数列.
(3)由(2)知a
n=n,则

.再用裂项求和法能够推导出实数a的取值范围.
点评:本题主要考查数列通项、求和与不等式等知识,考查化归与转化的数学思想方法,以及抽象概括能力、运算求解能力和创新意识

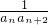 的前n项和为Sn,不等式
的前n项和为Sn,不等式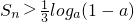 对任意的正整数n恒成立,求实数a的取值范围.
对任意的正整数n恒成立,求实数a的取值范围. .
.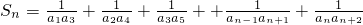 =
=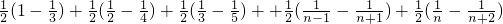 =
= =
=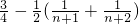 .
.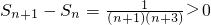 ,
,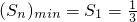 .
.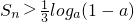 对任意正整数n恒成立,只要
对任意正整数n恒成立,只要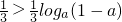 .
. .
. .
. .再用裂项求和法能够推导出实数a的取值范围.
.再用裂项求和法能够推导出实数a的取值范围.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案