
【题目】O为坐标原点,直线l与圆x2+y2=2相切.
(1)若直线l分别与x、y轴正半轴交于A、B两点,求△AOB面积的最小值及面积取得最小值时的直线l的方程.
(2)设直线l交椭圆 ![]() =1于P、Q两点,M为PQ的中点,求|OM|的取值范围.
=1于P、Q两点,M为PQ的中点,求|OM|的取值范围.
【答案】
(1)解:设直线l的方程为 ![]() =1(a,b>0),
=1(a,b>0),
由直线和圆x2+y2=4相切,可得 ![]() =
= ![]() ,
,
即有 ![]() =
= ![]() ≥
≥ ![]() ,即ab≥4,
,即ab≥4,
当且仅当a=b=2时,取得等号.
则△AOB面积S= ![]() ab的最小值为2;
ab的最小值为2;
此时直线的方程为x+y﹣2=0
(2)解:若直线的斜率不存在,设为x=t,
由直线和圆相切可得,t=﹣ ![]() 或
或 ![]() .
.
代入椭圆方程可得,y=± ![]() ,
,
可得中点M坐标为(﹣ ![]() ,0)或(
,0)或( ![]() ,0),|OM|=
,0),|OM|= ![]() ;
;
设直线l的方程为y=kx+m,代入椭圆方程可得,
(1+2k2)x2+4kmx+2m2﹣6=0,
△=16k2m2﹣4(1+2k2)(2m2﹣6)>0,
即为m2<3+6k2,
由直线和圆相切,可得 ![]() =
= ![]() ,
,
即为m2=2+2k2,由2+2k2<3+6k2,可得k∈R,
设P,Q的坐标为(x1,y1),(x2,y2),
可得x1+x2=﹣ ![]() ,中点M的坐标为(﹣
,中点M的坐标为(﹣ ![]() ,
, ![]() ),
),
即有|OM|= ![]() =
= ![]()
设1+2k2=t(t≥1),则|OM|= ![]() =
= ![]()
= ![]() ,由t≥1可得t=2取得最大值
,由t≥1可得t=2取得最大值 ![]() ,
,
t=1时,取得最小值 ![]() .
.
故|OM|的范围是[ ![]() ,
, ![]() ]
]
【解析】(1)设出直线方程,由直线和圆相切的条件:d=r,结合基本不等式,即可得到面积的最小值和此时直线的方程;(2)讨论直线的斜率不存在和存在,设出直线方程为y=kx+m,代入椭圆方程,运用韦达定理和中点坐标公式,结合判别式大于0,化简整理即可得到所求范围.


科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴的正半轴上,且半径为2的圆
轴的正半轴上,且半径为2的圆![]() 被直线
被直线![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设动直线![]() 与圆
与圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称?若存在,请求出点
轴对称?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.
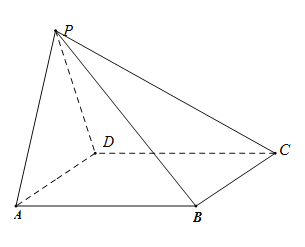
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《张丘建算经》是公元5世纪中国古代内容丰富的数学著作,书中卷上第二十三问:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈.问日益几何?”其意思为“有个女子织布,每天比前一天多织相同量的布,第一天织五尺,一个月(按30天计)共织390尺.问:每天多织多少布?”已知1匹=4丈,1丈=10尺,估算出每天多织的布的布约有( )
A.0.55尺
B.0.53尺
C.0.52尺
D.0.5尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的图象经过
的图象经过![]() 和
和![]() 两点,如图所示,且函数
两点,如图所示,且函数![]() 的值域为
的值域为![]() .过该函数图象上的动点
.过该函数图象上的动点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.

(I)求函数![]() 的解析式;
的解析式;
(Ⅱ)记![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() .
.
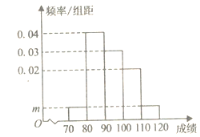
(1)求图中m的值;
(2)根据频率分布直方图,估计这200名学生的平均分(同一组中的数据用该组区间的中间值作代表)和中位数(四舍五入取整数);
(3)若这200名学生的数学成绩中,某些分数段的人数x与英语成绩相应分数段的人数y之比如下表所示,求英语成绩在![]() 的人数.
的人数.
分数段 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) |
x:y | 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com