
已知向量α,β,γ满足|α|=1,|α-β|=|β|,(α-γ)·(β-γ)=0.若对每一个确定的β,|γ|的最大值和最小值分别为m,n,则对任意β,m-n的最小值是( )
A.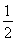 B.1 C.2 D.
B.1 C.2 D.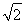
A
【解析】方法一,设α=(1,0),β=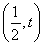 ,γ=(x,y),由(α-γ)·(β-γ)=0,得(x-1,y)
,γ=(x,y),由(α-γ)·(β-γ)=0,得(x-1,y)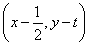 =0,即x2-
=0,即x2-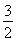 x+
x+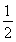 +y2-ty=0,配方得
+y2-ty=0,配方得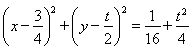 .|γ|的几何意义是圆上的点到坐标原点的距离,其最大值为圆心到坐标原点的距离加圆的半径,最小值为圆心到坐标原点的距离减去圆的半径,最大值与最小值之差为圆的直径,故m-n=2
.|γ|的几何意义是圆上的点到坐标原点的距离,其最大值为圆心到坐标原点的距离加圆的半径,最小值为圆心到坐标原点的距离减去圆的半径,最大值与最小值之差为圆的直径,故m-n=2 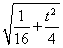 ≥
≥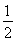 ,当且仅当t=0时等号成立,此时β=
,当且仅当t=0时等号成立,此时β=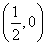 .
.
方法二,将向量α,β,γ的起点放在点O,终点分别记作A,B,C.由|α-β|=|β|可知点B在OA的垂直平分线上.根据(α-γ)·(β-γ)=0知点C在以AB为直径的圆上,则m-n为圆的直径.又因为OB=AB,故只要OB最小即得,结合图形,在点B为OA的中点时取得,即m-n的最小值为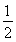 .
.



科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集3B讲练习卷(解析版) 题型:填空题
若正数x,y满足2x+y-3=0,则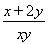 的最小值为________.
的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集2A讲练习卷(解析版) 题型:选择题
已知向量a=(1,1),2a+b=(4,2),则向量a,b的夹角的余弦值为( )
A. 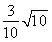 B.-
B.-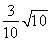 C.
C. 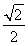 D.-
D.-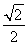
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集1A讲练习卷(解析版) 题型:选择题
定义集合运算A*B={z|z=xy+x+y,x∈A,y∈B}.已知P= ,Q={1,2},则P*Q=( )
,Q={1,2},则P*Q=( )
A.{-1,1,2,3,5} B.{-1,0,1,2}
C.{-1,1,2} D.{0,1,2,3}
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集19讲练习卷(解析版) 题型:解答题
已知函数f(x)=ln x-ax(a∈R).
(1)讨论函数f(x)的单调区间;
(2)若函数g(x)=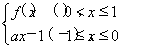 且g(x)≤1恒成立,求实数a的取值范围.
且g(x)≤1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集18讲练习卷(解析版) 题型:填空题
已知函数f(x)=2x+x,g(x)=x-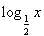 ,h(x)=log2x-
,h(x)=log2x-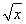 的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是______________.
的零点分别为x1,x2,x3,则x1,x2,x3的大小关系是______________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集17讲练习卷(解析版) 题型:填空题
从某项综合能力测试中抽取50人的成绩,统计如下表,则这50人成绩的方差为________.
分数 | 5 | 4 | 3 | 2 | 1 |
人数 | 10 | 5 | 15 | 15 | 5 |
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集14讲练习卷(解析版) 题型:解答题
设抛物线的顶点在原点,准线方程为x=-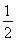 .
.
(1)求抛物线的标准方程;
(2)若点P是抛物线上的动点,点P在y轴上的射影是Q,点M ,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
,试判断|PM|+|PQ|是否存在最小值,若存在,求出其最小值,若不存在,请说明理由;
(3)过抛物线焦点F作互相垂直的两直线分别交抛物线于A,C,B,D,求四边形ABCD面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com