
【题目】某公司的两个部门招聘工作人员,应聘者从 T1、T2两组试题中选择一组参加测试,成绩合格者可签约.甲、乙、丙、丁四人参加应聘考试,其中甲、乙两人选择使用试题 T1 , 且表示只要成绩合格就签约;丙、丁两人选择使用试题 T2 , 并约定:两人成绩都合格就一同签约,否则两人都不签约.已知甲、乙考试合格的概率都是 ![]() ,丙、丁考试合格的概率都是
,丙、丁考试合格的概率都是 ![]() ,且考试是否合格互不影响. (I)求丙、丁未签约的概率;
,且考试是否合格互不影响. (I)求丙、丁未签约的概率;
(II)记签约人数为 X,求 X的分布列和数学期望EX.
【答案】解:(I)分别记事件甲、乙、丙、丁考试合格为 A,B,C,D. 由题意知 A,B,C,D相互独立,且 ![]() ,
, ![]() .
.
记事件“丙、丁未签约”为F,
由事件的独立性和互斥性得:
P(F)=1﹣P(CD)
= ![]()
(II) X的所有可能取值为0,1,2,3,4. ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以,X的分布列是:
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
X的数学期望 ![]()
【解析】(I)分别记事件甲、乙、丙、丁考试合格为 A,B,C,D.由题意知 A,B,C,D相互独立,且 ![]() ,
, ![]() .记事件“丙、丁未签约”为F,由事件的独立性和互斥性得能求出丙、丁未签约的概率.(II) X的所有可能取值为0,1,2,3,4,分别求出相应在的概率,由此能求出X的分布列和X的数学期望.
.记事件“丙、丁未签约”为F,由事件的独立性和互斥性得能求出丙、丁未签约的概率.(II) X的所有可能取值为0,1,2,3,4,分别求出相应在的概率,由此能求出X的分布列和X的数学期望.
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,边长为1的正方形![]() 中,
中,![]() 分别为边
分别为边![]() 上的点,且
上的点,且![]() 的周长为2.
的周长为2.

(1)求线段![]() 长度的最小值;
长度的最小值;
(2)试探究![]() 是否为定值,若是,给出这个定值;若不是,说明理由.
是否为定值,若是,给出这个定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点![]() ,直线l:
,直线l:![]() ,设圆C的半径为1,圆心C在直线l上.
,设圆C的半径为1,圆心C在直线l上.
![]() 过点A作圆C的切线AP且P为切点,当切线AP最短时,求圆C的标准方程;
过点A作圆C的切线AP且P为切点,当切线AP最短时,求圆C的标准方程;
![]() 若圆C上存在点M,使
若圆C上存在点M,使![]() ,求圆心C的横坐标a的取值范围.
,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两条平行直线和圆的位置关系定义为:若两条平行直线和圆有四个不同的公共点,则称两条平行线和圆“相交”;若两平行直线和圆没有公共点,则称两条平行线和圆“相离”;若两平行直线和圆有一个、两个或三个不同的公共点,则称两条平行线和圆“相切”.已知直线![]() ,
,![]() ,和圆:
,和圆:![]() 相切,则实数
相切,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() 或
或![]() B.
B. ![]() 或
或![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若四面体![]() 的三组对棱分别相等,即
的三组对棱分别相等,即![]() ,
,![]() ,
,![]() ,则________.(写出所有正确结论的编号)
,则________.(写出所有正确结论的编号)
①四面体![]() 每个面的面积相等
每个面的面积相等
②四面体![]() 每组对棱相互垂直
每组对棱相互垂直
③连接四面体![]() 每组对棱中点的线段相互垂直平分
每组对棱中点的线段相互垂直平分
④从四面体![]() 每个顶点出发的三条棱的长都可以作为一个三角形的三边长
每个顶点出发的三条棱的长都可以作为一个三角形的三边长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某学段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如右图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8. 
(1)将频率当作概率,请估计该学段学生中百米成绩在[16,17)内的人数以及所有抽取学生的百米成绩的中位数(精确到0.01秒);
(2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人用一网箱饲养中华鲟,研究表明:一个饲养周期,该网箱中华鲟的产量![]() (单位:百千克)与购买饲料费用
(单位:百千克)与购买饲料费用![]() (
(![]() )(单位:百元)满足:
)(单位:百元)满足:![]() .另外,饲养过程中还需投入其它费用
.另外,饲养过程中还需投入其它费用![]() .若中华鲟的市场价格为
.若中华鲟的市场价格为![]() 元/千克,全部售完后,获得利润
元/千克,全部售完后,获得利润![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为何值时,利润最大,最大利润是多少元?
为何值时,利润最大,最大利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知a1>1,an+1=an2﹣an+1(n∈N*),且 ![]()
![]() +…+
+…+ ![]() =2.则当a2016﹣4a1取得最小值时,a1的值为= .
=2.则当a2016﹣4a1取得最小值时,a1的值为= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客的购物总额(单位元),将数据按照
位顾客的购物总额(单位元),将数据按照![]()
![]() ,
,![]()
![]() 分成
分成![]() 组,制成了如下图所示的频率分布直方图:
组,制成了如下图所示的频率分布直方图:
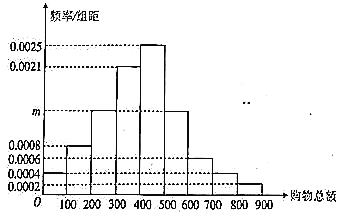
该商场每日大约有![]() 名顾客,为了增加商场销售总额,近期对一次性购物不低于
名顾客,为了增加商场销售总额,近期对一次性购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(1)求频率分布直方图中![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(2)若每日按分层抽样的方法从购物总额在![]() 三组对应的顾客中抽取
三组对应的顾客中抽取![]() 名顾客,这
名顾客,这![]() 名顾客中再随机抽取两名超级顾客,每人奖励一个超级礼包,求获得超级礼包的两人来自不同组的概率.
名顾客中再随机抽取两名超级顾客,每人奖励一个超级礼包,求获得超级礼包的两人来自不同组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com