
【题目】如图所示,在直三棱柱![]() 中,平面
中,平面![]() 侧面
侧面![]() ,且
,且![]() .
.

(1)求证:![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求锐二面角
,求锐二面角![]() 的大小.
的大小.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由已知条件推导出
,由已知条件推导出![]() 平面
平面![]() ,从而得到
,从而得到![]() ,由线面垂直得
,由线面垂直得![]() ,由此可证明
,由此可证明![]() ;(2)连接
;(2)连接![]() ,由(1)可知
,由(1)可知![]() 平面
平面![]() ,由已知条件得到
,由已知条件得到![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角,
所成的角,![]() 即二面角
即二面角![]() 的一个平面角,即可求解二面角的大小.
的一个平面角,即可求解二面角的大小.
试题解析:(1)如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
由平面![]() 侧面
侧面![]() ,且平面
,且平面![]() 侧面
侧面![]() 得
得![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() .
.
因为三棱柱![]() 是直三棱柱,则
是直三棱柱,则![]() 底面
底面![]() .又因为
.又因为![]() 平面
平面![]() ,
,
所以![]() .又
.又![]() ,所以
,所以![]() 侧面
侧面![]() ,
,
又![]() 侧面
侧面![]() ,故
,故![]() .
.

(2)连接![]() ,由(1)可知
,由(1)可知![]() 平面
平面![]() ,则
,则![]() 是
是![]() 在平面
在平面![]() 内的射影,
内的射影,
所以![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角,
所成的角,
因为直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,所以
,所以![]() ,
,
在等腰直角![]() 中,
中,![]() 且点
且点![]() 是
是![]() 中点,所以
中点,所以![]() .
.
又![]() ,所以
,所以![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,
由(1)知![]() 平面
平面![]() ,则
,则![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() ,所以
,所以![]() 即二面角
即二面角![]() 的一个平面角.且直角
的一个平面角.且直角![]() 中,
中,![]() .又
.又![]() ,
,
所以![]() .又因为二面角
.又因为二面角![]() 为锐二面角,
为锐二面角,
所以![]() .即锐二面角
.即锐二面角![]() 的大小为
的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行![]() 天试销,每种单价试销
天试销,每种单价试销![]() 天,得到如下数据:
天,得到如下数据:
单价 |
|
|
|
|
|
销量 |
|
|
|
|
|
(1)求试销![]() 天的销量的方差和
天的销量的方差和![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是![]() 元,
元,
为了获得最大利润,该单元卷的单价应定为多少元?
附:  ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某公司技术升级后生产![]() 产品过程中记录的产量
产品过程中记录的产量![]() (吨)与相应的成本
(吨)与相应的成本![]() (万元)的几组对照数据:
(万元)的几组对照数据:

(1)请画出上表数据的散点图;

(2)请根据上表提供的数据,用最小二乘法求出![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(3)已知该公司技术升级前生产100吨![]() 产品的成本为90万元.试根据(2)求出的回归直线方程,预测技术升级后生产100吨
产品的成本为90万元.试根据(2)求出的回归直线方程,预测技术升级后生产100吨![]() 产品的成本比技术升级前约降低多少万元?
产品的成本比技术升级前约降低多少万元?
(附:  ,
, ![]() ,其中
,其中![]() 为样本平均值)
为样本平均值)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD-A1B1C1D中,S是B1D1的中点,E、F、G分别是BC、CD和SC的中点.求证:
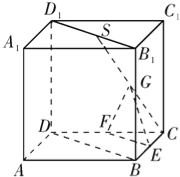
(1)直线EG∥平面BDD1B1;
(2)平面EFG∥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:![]() 与圆O:
与圆O:![]() 相交于A,B两个不同的点,且A
相交于A,B两个不同的点,且A![]() ,B
,B![]() .
.
(1)当![]() 面积最大时,求m的取值,并求出
面积最大时,求m的取值,并求出![]() 的长度.
的长度.
(2)判断![]() 是否为定值;若是,求出定值的大小;若不是,说明理由.
是否为定值;若是,求出定值的大小;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高中生上学使用手机情况,调查者进行了如下的随机调查:调查者向被调查者提出两个问题:(1)你的学号是奇数吗?(2)你上学时是否经常带手机?要求被调查者背对着调查人员抛掷一枚硬币,如果出现正面,就回答第一问题,否则就回答第二个问题.被调查者不必告诉调查人员自己回答的是哪一个问题,只需回答“是”或“不是”,因为只有被调查者本人知道回答了哪一个问题,所以都如实地做了回答.结果被调查的800人(学号从1至800)中有260人回答了“是”.由此可以估计这800人中经常带手机上学的人数是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)将函数![]() 的图像向左平移
的图像向左平移![]() 个单位后,再将图像上各点的横坐标伸长到原来的
个单位后,再将图像上各点的横坐标伸长到原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图像,求
的图像,求![]() 的最大值及取得最大值时的
的最大值及取得最大值时的![]() 的集合.
的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于某设备的使用年限![]() 和所支出的维修费用
和所支出的维修费用![]() (万元),有如下的统计资料:
(万元),有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)如由资料可知![]() 对
对![]() 呈线形相关关系.试求:线形回归方程;(
呈线形相关关系.试求:线形回归方程;(![]() ,
, )
)
(2)估计使用年限为10年时,维修费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com