
【题目】天干地支纪年法,源于中国,中国自古便有十天干与十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天干回到“甲”重新开始,即“甲戌”,“乙亥”,之后地支回到“子”重新开始,即“丙子”,…,以此类推,已知2016年为丙申年,那么到改革开放100年时,即2078年为________年
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程![]() ,变量x增加一个单位时,y平均增加5个单位;
,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程![]() 必过
必过![]() ;
;
④在一个![]() 列联表中,由计算得是
列联表中,由计算得是![]() ,则有
,则有![]() 的把握确认这两个变量间有关系.
的把握确认这两个变量间有关系.
其中错误的个数是( )
本题可以参考独立性检验临界值表:
| 0.05 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)![]() ,函数g(θ)=cos2θ+2sinθ
,函数g(θ)=cos2θ+2sinθ![]() ,θ∈[m,
,θ∈[m,![]() ].m,b∈R.
].m,b∈R.
(1)求b的值;
(2)判断函数f(x)在[0,1]上的单调性,并证明;
(3)当x∈[0,1]时,函数g(θ)的最小值恰为f(x)的最大值,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,且过点
轴上,且过点![]() ,若
,若![]() 的两焦点与其中一个顶点能构成一个等边三角形.
的两焦点与其中一个顶点能构成一个等边三角形.
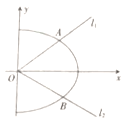
(1)求![]() 的方程.
的方程.
(2)已知过![]() 的两条直线
的两条直线![]() ,
,![]() (斜率都存在)与
(斜率都存在)与![]() 的右半部分(
的右半部分(![]() 轴右侧)分别相交于
轴右侧)分别相交于![]() ,
,![]() 两点,且
两点,且![]() 的面积为
的面积为![]() ,试判断
,试判断![]() ,
,![]() 的斜率之积是否为定值?若是,求出定值;若不是,说明理由.
的斜率之积是否为定值?若是,求出定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高速公路服务区临时停车场按时段收费,收费标准:每辆汽车一次停车不超过1小时收费5元,超过1小时的部分每小时收费7元(不足1小时的部分按1小时计算).现有甲、乙两人在该服务区临时停车,两人停车都不超过4小时.
(1)若甲停车1小时以上且不超过2小时的概率为![]() ,停车付费多于12元的概率为
,停车付费多于12元的概率为![]() ,求甲停车付费恰为5元的概率;
,求甲停车付费恰为5元的概率;
(2)若每人停车的时长在每个时段的可能性相同,求甲、乙两人停车付费之和为38元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称数列
,则称数列![]() 是“回归数列”.
是“回归数列”.
(1)前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(2)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值;
的值;
(3)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() (
(![]() )成立,请给出你的结论,并说明理由.
)成立,请给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阶梯水价的原则是“保基本、建机制、促节约”,其中“保基本”是指保证至少80%的居民用户用水价格不变.为响应国家政策,制订合理的阶梯用水价格,某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研,得到数据如下(单位:吨).
郊区:19 25 28 32 34
城区:18 19 21 22 22 23 23 23 24 25 26 27 28 28 28 29 29 31 35 42
(1)在郊区的这5户居民中随机抽取2户,求其年人均用水量都不超过30吨的概率;
(2)设该城市郊区和城区的居民户数比为1:5,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,并保证这一阶梯的居民用户用水价格保持不变,试根据样本总体的思想,分析此方案是否符合国家“保基本”政策.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】12个朋友每周聚餐一次,每周他们分成三组,每组4人,不同组坐不同的桌子.若要求这些朋友中任意两个人至少有一次同坐一张桌子,则至少需要周____周.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com