
【题目】如果数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等差数列”,
是“间等差数列”,![]() 为“间公差”.若数列
为“间公差”.若数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)求证:数列![]() 是“间等差数列”,并求间公差
是“间等差数列”,并求间公差![]() ;
;
(2)设![]() 为数列
为数列![]() 的前n项和,若
的前n项和,若![]() 的最小值为-153,求实数
的最小值为-153,求实数![]() 的取值范围;
的取值范围;
(3)类似地:非零数列![]() 对于任意
对于任意![]() ,都有
,都有![]() ,其中
,其中![]() 为常数,则称数列
为常数,则称数列![]() 是“间等比数列”,
是“间等比数列”,![]() 为“间公比”.已知数列
为“间公比”.已知数列![]() 中,满足
中,满足![]() ,
,![]() ,
,![]() ,试问数列
,试问数列![]() 是否为“间等比数列”,若是,求最大的整数
是否为“间等比数列”,若是,求最大的整数![]() 使得对于任意
使得对于任意![]() ,都有
,都有![]() ;若不是,说明理由.
;若不是,说明理由.
【答案】(1)见解析;(2)![]() ;(3)63.
;(3)63.
【解析】
(1)直接利用定义求出数列为间等差数列.
(2)利用分类讨论思想,利用数列的前n项和公式求出数列的和,进一步利用不等量关系求出结果.
(3)利用分类讨论思想,进一步求出数列的通项公式,再利用函数的单调性求出k的最大值.
(1)若数列{an}满足an+an+1=2n﹣35,n∈N*,则:an+1+an+2=2(n+1)﹣35,
两式相减得:an+2﹣an=2.故数列{an}是“间等差数列”,公差d=2.
(2)(i)当n=2k时,
![]() (a1+a2)+(a3+a4)+…+(an﹣1+an)=﹣33﹣29+…+(2n﹣37)=
(a1+a2)+(a3+a4)+…+(an﹣1+an)=﹣33﹣29+…+(2n﹣37)=![]()
易知:当n=18时,最小值S18=﹣153.
(ii)当n=2k+1时,
Sn=a1+(a2+a3)+(a4+a5)+…+(an﹣1+an)=a1+(﹣31)+(﹣29)+…+(2n﹣37)=![]() ,
,
当n=17时最小,其最小值为S17=a﹣136,要使其最小值为﹣153,
则:a﹣136≥﹣153,解得:a≥﹣17.
(3)易知:cncn+1=2018(![]() )n﹣1,则:cn+1cn+2=2018(
)n﹣1,则:cn+1cn+2=2018(![]() )n,
)n,
两式相除得:![]() ,故数列{cn}为“间等比数列”,其间等比为
,故数列{cn}为“间等比数列”,其间等比为![]() .
.![]() ,
,
易求出数列的通项公式为: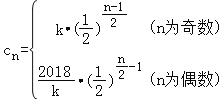 ,
,
由于![]() n>
n>![]() n+1,则数列{
n+1,则数列{![]() n}单调递减.那么,奇数项和偶数项都为单调递减,所以:k>0.
n}单调递减.那么,奇数项和偶数项都为单调递减,所以:k>0.
要使数列为单调递减数列.只需![]() 2m﹣1>
2m﹣1>![]() 2m>
2m>![]() 2m+1,
2m+1,
即:![]() ,
,
解得![]() ,即最大的整数
,即最大的整数![]() .
.


科目:高中数学 来源: 题型:
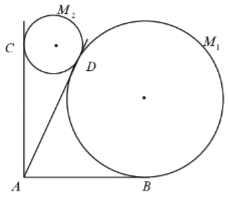
【题目】某景区欲建两条圆形观景步道![]() (宽度忽略不计),如图所示,已知
(宽度忽略不计),如图所示,已知![]() ,
,![]() (单位:米),要求圆M与
(单位:米),要求圆M与![]() 分别相切于点B,D,圆
分别相切于点B,D,圆![]() 与
与![]() 分别相切于点C,D.
分别相切于点C,D.
(1)若![]() ,求圆
,求圆![]() 的半径;(结果精确到0.1米)
的半径;(结果精确到0.1米)
(2)若观景步道![]() 的造价分别为每米0.8千元与每米0.9千元,则当
的造价分别为每米0.8千元与每米0.9千元,则当![]() 多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
多大时,总造价最低?最低总造价是多少?(结果分别精确到0.1°和0.1千元)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.

(1)求证:AB⊥平面PCB;
(2)求二面角C﹣PA﹣B的大小的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)若![]() 满足
满足![]() 为
为![]() 上奇函数且
上奇函数且![]() 为
为![]() 上偶函数,求
上偶函数,求![]() 的值;
的值;
(2)若函数![]()
![]() 满足
满足![]() 对
对![]() 恒成立,函数
恒成立,函数![]() ,求证:函数
,求证:函数![]() 是周期函数,并写出
是周期函数,并写出![]() 的一个正周期;
的一个正周期;
(3)对于函数![]() ,
,![]()
![]() ,若
,若![]() 对
对![]() 恒成立,则称函数
恒成立,则称函数![]() 是“广义周期函数”,
是“广义周期函数”, ![]() 是其一个广义周期,若二次函数
是其一个广义周期,若二次函数![]() 的广义周期为
的广义周期为![]() (
(![]() 不恒成立),试利用广义周期函数定义证明:对任意的
不恒成立),试利用广义周期函数定义证明:对任意的![]() ,
,![]() ,
,![]() 成立的充要条件是
成立的充要条件是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某斜拉式大桥图片,为了了解桥的一些结构情况,学校数学兴趣小组将大桥的结构进行了简化,取其部分可抽象成图2所示的模型,其中桥塔![]() 、
、![]() 与桥面
与桥面![]() 垂直,通过测量得知
垂直,通过测量得知![]() ,
,![]() ,当
,当![]() 为
为![]() 中点时,
中点时,![]() .
.
(1)求![]() 的长;
的长;
(2)试问![]() 在线段
在线段![]() 的何处时,
的何处时,![]() 达到最大.
达到最大.

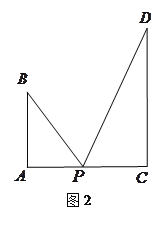
图1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《上海市生活垃圾管理条例》于2019年7月1日正式实施,某小区全面实施垃圾分类处理,已知该小区每月垃圾分类处理量不超过300吨,每月垃圾分类处理成本![]() (元)与每月分类处理量
(元)与每月分类处理量![]() (吨)之间的函数关系式可近似表示为
(吨)之间的函数关系式可近似表示为![]() ,而分类处理一吨垃圾小区也可以获得300元的收益.
,而分类处理一吨垃圾小区也可以获得300元的收益.
(1)该小区每月分类处理多少吨垃圾,才能使得每吨垃圾分类处理的平均成本最低;
(2)要保证该小区每月的垃圾分类处理不亏损,每月的垃圾分类处理量应控制在什么范围?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记无穷数列![]() 的前
的前![]() 项中最大值为
项中最大值为![]() ,最小值为
,最小值为![]() ,令
,令![]()
(Ⅰ)若![]() ,请写出
,请写出![]() 的值;
的值;
(Ⅱ)求证:“数列![]() 是等差数列”是“数列
是等差数列”是“数列![]() 是等差数列”的充要条件;
是等差数列”的充要条件;
(Ⅲ)若![]() ,求证:存在
,求证:存在![]() ,使得
,使得![]() ,有
,有![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com