
【题目】2017年春晚过后,为了研究演员上春晚次数与受关注度的关系,某网站对其中一位经常上春晚的演员上春晚次数与受关注度进行了统计,得到如下数据:
上春晚次数x(单位:次) | 2 | 4 | 6 | 8 | 10 |
粉丝数量y(单位:万人) | 10 | 20 | 40 | 80 | 100 |
(1)若该演员的粉丝数量g(x)≤g(1)=0与上春晚次数x满足线性回归方程,试求回归方程 ![]() =
= ![]() x+
x+ ![]() ,并就此分析,该演员上春晚12次时的粉丝数量;
,并就此分析,该演员上春晚12次时的粉丝数量;
(2)若用 ![]() (i=1,2,3,4,5)表示统计数据时粉丝的“即时均值”(四舍五入,精确到整数),从这5个“即时均值”中任选2数,记所选的2数之和为随机变量η,求η的分布列与数学期望. 参考公式:
(i=1,2,3,4,5)表示统计数据时粉丝的“即时均值”(四舍五入,精确到整数),从这5个“即时均值”中任选2数,记所选的2数之和为随机变量η,求η的分布列与数学期望. 参考公式: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
【答案】
(1)解:由题意可知,
计算 ![]() =
= ![]() ×(2+4+6+8+10)=6,
×(2+4+6+8+10)=6,
![]() =
= ![]() ×(10+20+40+80+100)=50;
×(10+20+40+80+100)=50;
回归系数为
![]() =
= 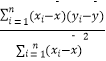 =
= ![]() =12,
=12,
![]() =
= ![]() ﹣
﹣ ![]() =50﹣12×6=﹣22,
=50﹣12×6=﹣22,
∴回归方程为 ![]() =12x﹣22;
=12x﹣22;
当x=12时, ![]() =12×12﹣22=122,
=12×12﹣22=122,
所以该演员上春晚12次时的粉丝数约为122万人
(2)解:经计算可知,这五个“即时均值”分别为:5、5、7、10、10,
∴η的可能取值有10、12、15、17、20;
计算P(η=10)= ![]() ,P(η=12)=
,P(η=12)= ![]() ,
,
P(η=15)= ![]() ,P(η=17)=
,P(η=17)= ![]() ,
,
P(η=20)= ![]() ;
;
∴η的分布列为:
η | 10 | 12 | 15 | 17 | 20 |
P | | | |
| |
∴数学期望为E(η)=10× ![]() +12×
+12× ![]() +15×
+15× ![]() +17×
+17× ![]() +20×
+20× ![]() =
= ![]()
【解析】(1)由题意,计算 ![]() 、
、 ![]() ,求出回归系数,写出回归方程,计算x=12时
,求出回归系数,写出回归方程,计算x=12时 ![]() 的方程即可;(2)经计算可知这五个“即时均值”分别为:5、5、7、10、10, 得出η的可能取值,计算对应的概率值,写出η的分布列,计算数学期望值.
的方程即可;(2)经计算可知这五个“即时均值”分别为:5、5、7、10、10, 得出η的可能取值,计算对应的概率值,写出η的分布列,计算数学期望值.
【考点精析】根据题目的已知条件,利用离散型随机变量及其分布列的相关知识可以得到问题的答案,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的最小正周期为π,将函数f(x)的图象向右平移
的最小正周期为π,将函数f(x)的图象向右平移 ![]() 个所得图象对应的函数为y=g(x),则关于函数为y=g(x)的性质,下列说法不正确的是( )
个所得图象对应的函数为y=g(x),则关于函数为y=g(x)的性质,下列说法不正确的是( )
A.g(x)为奇函数
B.关于直线 ![]() 对称
对称
C.关于点(π,0)对称
D.在 ![]() 上递增
上递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的方程为x﹣y+4=0,曲线C的参数方程为 ![]() .
.
(1)已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为 ![]() ,判断点P与直线l的位置关系;
,判断点P与直线l的位置关系;
(2)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}为等差数列,a1=3且(a3﹣1)是(a2﹣1)与a4的等比中项.
(1)求an;
(2)若数列{an}的前n项和为Sn , bn= ![]() ,Tn=﹣b1+b2+b3+…+(﹣1)nbn , 求Tn .
,Tn=﹣b1+b2+b3+…+(﹣1)nbn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在定义域R上的导函数为f′(x),若方程f'(x)=0无解,且f[f(x)﹣2017x]=2017,当g(x)=sinx﹣cosx﹣kx在[﹣ ![]() ,
, ![]() ]上与f(x)在R上的单调性相同时,则实数k的取值范围是( )
]上与f(x)在R上的单调性相同时,则实数k的取值范围是( )
A.(﹣∞,﹣1]
B.(﹣∞, ![]() ]
]
C.[﹣1, ![]() ]
]
D.[ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若集合A={x|2 ![]() >1},集合B={x|y=lg
>1},集合B={x|y=lg ![]() },则A∩B=( )
},则A∩B=( )
A.{x|﹣5<x<1}
B.{x|﹣2<x<1}
C.{x|﹣2<x<﹣1}
D.{x|﹣5<x<﹣1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x)﹣x﹣ax2 , a∈R. (Ⅰ)若函数f(x)在区间 ![]() 上有单调递增区间,求实数a的取值范围;
上有单调递增区间,求实数a的取值范围;
(Ⅱ)证明不等式: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数 ![]() 图象上所有点的横坐标缩短为原来的
图象上所有点的横坐标缩短为原来的 ![]() ,纵坐标不变,再向右平移
,纵坐标不变,再向右平移 ![]() 个单位长度,得到函数y=g(x)的图象,则下列说法正确的是( )
个单位长度,得到函数y=g(x)的图象,则下列说法正确的是( )
A.函数g(x)的一条对称轴是 ![]()
B.函数g(x)的一个对称中心是 ![]()
C.函数g(x)的一条对称轴是 ![]()
D.函数g(x)的一个对称中心是 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列{an}的各项都是正数,其前n项和为Sn , 且满足:a1=a,rSn=anan+1﹣1,其中a≠1,常数r∈N;
(1)求证:an+2﹣an是一个定值;
(2)若数列{an}是一个周期数列(存在正整数T,使得对任意n∈N* , 都有an+T=an成立,则称{an}为周期数列,T为它的一个周期,求该数列的最小周期;
(3)若数列{an}是各项均为有理数的等差数列,cn=23n﹣1(n∈N*),问:数列{cn}中的所有项是否都是数列{an}中的项?若是,请说明理由,若不是,请举出反例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com