
【题目】设函数f(x)=x2﹣2|x|﹣1(﹣3≤x≤3),
(1)画出这个函数的图象;
(2)指出函数f(x)的单调区间,并说明在各个单调区间上f(x)是增函数还是减函数;
(3)求函数的值域.
【答案】
(1)解:当x≥0时,f(x)=x2﹣2x﹣1=(x﹣1)2﹣2,
当x<0时,f(x)=x2+2x﹣1=(x+1)2﹣2,
根据二次函数的作图方法,可得函数图象如图
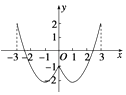
(2)解:函数f(x)的单调区间为
[﹣3,﹣1),[﹣1,0),[0,1),[1,3].
f(x)在区间[﹣3,﹣1)和[0,1)上为减函数,
在[﹣1,0),[1,3]上为增函数
(3)解:当x≥0时,函数f(x)=(x﹣1)2﹣2的最小值为﹣2,
最大值为f(3)=2;
当x<0时,函数f(x)=(x+1)2﹣2的最小值为﹣2,
最大值为f(﹣3)=2.
故函数f(x)的值域为[﹣2,2]
【解析】(1)化为分段函数,根据二次函数的作图方法,可得函数图象如图.(2)由图象可得函数得到f(x)的单调区间,(3)由图象可得函数的值域.


科目:高中数学 来源: 题型:
【题目】某地区山体大面积滑坡,政府准备调运一批赈灾物资共装26辆车,从某市出发以v(km/h)的速度匀速直达灾区,如果两地公路长400km,且为了防止山体再次坍塌,每两辆车的间距保持在( ![]() )2km.(车长忽略不计)设物资全部运抵灾区的时间为y小时,请建立y关于每车平均时速v(km/h)的函数关系式,并求出车辆速度为多少千米/小时,物资能最快送到灾区?
)2km.(车长忽略不计)设物资全部运抵灾区的时间为y小时,请建立y关于每车平均时速v(km/h)的函数关系式,并求出车辆速度为多少千米/小时,物资能最快送到灾区?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂生产的某种化工产品,当年产量在150吨至250吨之间,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可近似地表示为 ![]()
问:
(1)年产量为多少吨时,每吨的平均成本最低?并求出最低成本?
(2)若每吨平均出厂价为16万元,则年产量为多少吨时,可获得最大利润?并求出最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知U={1,2,3,4,5,6,7,8},A={1,3,5,7},B={2,4,5}则U(A∪B)( )
A.{6,8}
B.{5,7}
C.{4,6,7}
D.{1,3,5,6,8}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y. 
(1)写出y关于x的函数关系式,并指出这个函数的定义域.
(2)当AE为何值时,绿地面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (a>0,a≠1).
(a>0,a≠1).
(1)求函数f(x)的定义域;
(2)讨论函数f(x)的奇偶性;
(3)求a的取值范围,使f(x)+f(2x)>0在其定义域上恒成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com