③④
分析:通过举反例可得①不正确;利用函数的图象和性质可得②不正确;
根据y=tanx的图象的对称中心是(

,0),k∈Z,可得③正确;
对于④:利用直接法求解.为了求函数的一个单调递减区间,必须考虑到1+2cos2x>0并且使得内函数u=1+2cos2x是减函数才行,据此即可求得单调区间,从而进行判断;
根据利用左加右减上加下减的平移原则,直接求出函数y=3sin2x的图象经过平移而得到,函数y=3sin(2x+

)的图象的方法,可得⑤不正确.
解答:由于390°>30°,且都是第一象限角,sin390°=sin30°=

,
故函数y=sinx在第一象限不是增函数,故①不正确.
函数y=|cosx+

|的图象如下,故函数y=|cosx+

|的周期为2π,故②不正确;
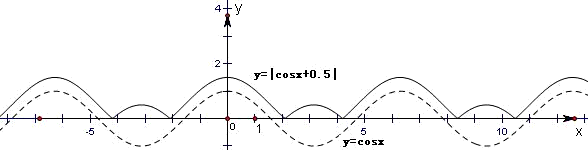
对于③:由于函数y=tanx的图象的对称中心是(

,0),k∈Z,
令

=

,∴x=kπ,故函数y=tan

的图象的对称中心是(kπ,0),k∈Z,正确.
④∵1+2cos2x>0且使得函数u=1+2cos2x是减函数,
∴2kπ≤2x<

+2kπ(k∈Z)?kπ≤x<

+kπ,
故函数y=ln(1+2cos2x)的递减区间是[kπ,kπ+

),k∈Z,④正确.
⑤:函数y=3sin2x的图象经过向左平移

,而得到函数y=3sin[2(x+

)]=3sin(2x+

),就是函数y=3sin(2x+

)的图象,故⑤不正确.
故答案为:③④.
点评:本题主要考查三角函数的图象和性质的应用,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法.

 |的最小正周期是π;
|的最小正周期是π; x的图象的对称中心是(kπ,0),k∈Z;
x的图象的对称中心是(kπ,0),k∈Z; ),k∈Z;
),k∈Z; )的图象可由函数y=3sin2x的图象向右平移
)的图象可由函数y=3sin2x的图象向右平移 平移得到.
平移得到. ,0),k∈Z,可得③正确;
,0),k∈Z,可得③正确; )的图象的方法,可得⑤不正确.
)的图象的方法,可得⑤不正确. ,
, |的图象如下,故函数y=|cosx+
|的图象如下,故函数y=|cosx+ |的周期为2π,故②不正确;
|的周期为2π,故②不正确;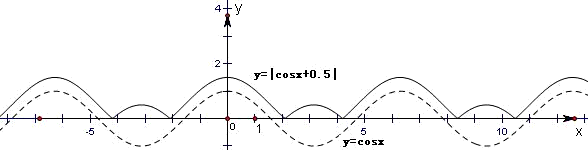
 ,0),k∈Z,
,0),k∈Z, =
= ,∴x=kπ,故函数y=tan
,∴x=kπ,故函数y=tan 的图象的对称中心是(kπ,0),k∈Z,正确.
的图象的对称中心是(kπ,0),k∈Z,正确. +2kπ(k∈Z)?kπ≤x<
+2kπ(k∈Z)?kπ≤x< +kπ,
+kπ, ),k∈Z,④正确.
),k∈Z,④正确. ,而得到函数y=3sin[2(x+
,而得到函数y=3sin[2(x+ )]=3sin(2x+
)]=3sin(2x+ ),就是函数y=3sin(2x+
),就是函数y=3sin(2x+ )的图象,故⑤不正确.
)的图象,故⑤不正确.
