
【题目】在△ABC中,内角A、B、C所对的边分别是a、b、c,已知3asinC=ccosA.
(Ⅰ)求sinA的值;
(Ⅱ)若B= ![]() ,△ABC的面积为9,求a的值.
,△ABC的面积为9,求a的值.
【答案】解:(Ⅰ)∵3asinC=ccosA.
∴2sinAsinC=sinCcosA,
∵sinC≠0,
∴tanA= ![]() ,且A为锐角,
,且A为锐角,
∴sinA= ![]() …7分
…7分
(Ⅱ)由(Ⅰ)可得cosA= ![]() =
= ![]() ,
,
∴sinC=sin(A+B)=sin(A+ ![]() )=
)= ![]() ,
,
由正弦定理可得 ![]() =
= ![]() ,c=2
,c=2 ![]() a,
a,
∵S= ![]() acsinB=
acsinB= ![]() =a2=9,
=a2=9,
∴a=3
【解析】(Ⅰ)由已知及正弦定理可得2sinAsinC=sinCcosA,由于sinC≠0,可求tanA= ![]() ,且A为锐角,利用同角三角函数基本关系式可求sinA的值.(Ⅱ)利用同角三角函数基本关系式可求可得cosA,利用两角和的正弦函数公式可求sinC,由正弦定理可得c=2
,且A为锐角,利用同角三角函数基本关系式可求sinA的值.(Ⅱ)利用同角三角函数基本关系式可求可得cosA,利用两角和的正弦函数公式可求sinC,由正弦定理可得c=2 ![]() a,进而利用三角形面积公式即可计算得解.
a,进而利用三角形面积公式即可计算得解.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知f(x)=e2x+ln(x+a).
(1)当a=1时,①求f(x)在(0,1)处的切线方程;②当x≥0时,求证:f(x)≥(x+1)2+x.
(2)若存在x0∈[0,+∞),使得 ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +
+ ![]() =1两焦点分别为F1、F2 , P是椭圆在第一象限弧上一点,并满足
=1两焦点分别为F1、F2 , P是椭圆在第一象限弧上一点,并满足 ![]()
![]() =1,过P作两条直线PA、PB分别交椭圆于A、B两点.
=1,过P作两条直线PA、PB分别交椭圆于A、B两点.
(1)求P点坐标;
(2)若直线AB的斜率为 ![]() ,求△PAB面积的最大值.
,求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a、b、c分别为角ABC所对的边,且 ![]() acosC=csinA.
acosC=csinA.
(1)求角C的大小.
(2)若c=2 ![]() ,且△ABC的面积为6
,且△ABC的面积为6 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinxcos2x,则下列关于函数f(x)的结论中,错误的是( )
A.最大值为1
B.图象关于直线x=﹣ ![]() 对称
对称
C.既是奇函数又是周期函数
D.图象关于点( ![]() ,0)中心对称
,0)中心对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体ABCD中,二面角A﹣BC﹣D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( ) 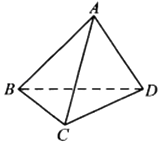
A.θ的最大值为60°
B.θ的最小值为60°
C.θ的最大值为30°
D.θ的最小值为30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.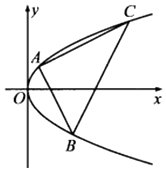
(Ⅰ)若A(1,2),B(4,﹣4),求点C的坐标;
(Ⅱ)若抛物线上存在点D,使得线段AD总被直线BC平分,求点A的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了解用电量y与气温x℃之间的关系,随机统计了5天的用电量与当天气温,得到如下统计表:
曰期 | 8月1曰 | 8月7日 | 8月14日 | 8月18日 | 8月25日 |
平均气温(℃) | 33 | 30 | 32 | 30 | 25 |
用电量(万度) | 38 | 35 | 41 | 36 | 30 |
![]() xiyi=5446,
xiyi=5446, ![]() xi2=4538,
xi2=4538, ![]() =
= 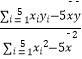 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
(1)请根据表中的数据,求出y关于x的线性回归方程.据气象預报9月3日的平均气温是 23℃,请预测9月3日的用电量;(结果保留整数)
(2)请从表中任选两天,记用电量(万度)超过35的天数为ξ,求ξ的概率分布列,并求其数学期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC, ![]() ,AB⊥AC,D是棱BB1的中点.
,AB⊥AC,D是棱BB1的中点. 
(Ⅰ)证明:平面A1DC⊥平面ADC;
(Ⅱ)求平面A1DC与平面ABC所成二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com