
【题目】设全集![]() ,关于
,关于![]() 的不等式
的不等式![]() (
(![]() )的解集为
)的解集为![]() .
.
(1)求集合![]() ;
;
(2)设集合![]() ,若
,若![]() 中有且只有三个元素,求实数
中有且只有三个元素,求实数![]() 的取值范围.
的取值范围.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】若![]() 是一个集合,
是一个集合,![]() 是一个以
是一个以![]() 的某些子集为元素的集合,且满足:(1)
的某些子集为元素的集合,且满足:(1)![]() 属于
属于![]() ,
,![]() 属于
属于![]() ;(2)
;(2)![]() 中任意多个元素的并集属于
中任意多个元素的并集属于![]() ;(3)
;(3)![]() 中任意多个元素的交集属于
中任意多个元素的交集属于![]() ,则称
,则称![]() 是集合
是集合![]() 上的一个拓补.已知集合
上的一个拓补.已知集合![]() ,对于下面给出的四个集合
,对于下面给出的四个集合![]() :
:
①![]() ②
②![]()
③![]() ④
④![]()
其中是集合![]() 上的拓补的集合
上的拓补的集合![]() 的序号是______.(写出所有的拓补的集合
的序号是______.(写出所有的拓补的集合![]() 的序号)
的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于自然数数组![]() ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果![]() 的极差
的极差![]() ,可实施如下操作
,可实施如下操作![]() :若
:若![]() 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若![]() 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为
中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为![]() ,其级差为
,其级差为![]() .若
.若![]() ,则继续对
,则继续对![]() 实施操作
实施操作![]() ,…,实施
,…,实施![]() 次操作后的结果记为
次操作后的结果记为![]() ,其极差记为
,其极差记为![]() .例如:
.例如:![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知![]() 的极差为
的极差为![]() 且
且![]() ,若
,若![]() 时,恒有
时,恒有![]() ,求
,求![]() 的所有可能取值;
的所有可能取值;
(3)若![]() 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在![]() 满足
满足![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由正方形![]() ,直角梯形
,直角梯形![]() ,三角形
,三角形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
,![]() ,将其沿
,将其沿![]() ,
,![]() 折起使得
折起使得![]() 与
与![]() 重合,连接
重合,连接![]() ,如图2.
,如图2.
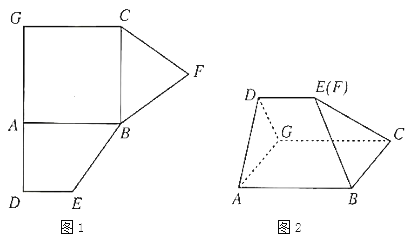
(1)证明:图2中的![]() ,
,![]() ,
,![]() ,
,![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在开展创建“全国文明城市”活动中,工作有序扎实,成效显著,尤其是城市环境卫生大为改观,深得市民好评.“创文”过程中,某网站推出了关于环境治理和保护问题情况的问卷调查,现从参与问卷调查的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
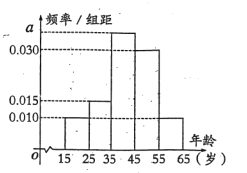
(1)求出a的值;
(2)若已从年龄较小的第1,2组中用分层抽样的方法抽取5人,现要再从这5人中随机抽取3人进行问卷调查,设第2组抽到![]() 人,求随机变量
人,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() 的左顶点为
的左顶点为![]() ,且椭圆
,且椭圆![]() 经过点
经过点![]() ,与坐标轴不垂直的直线
,与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 和直线
和直线![]() 的斜率之积为
的斜率之积为![]() ,求证:直线
,求证:直线![]() 过定点;
过定点;
(3)若![]() 为椭圆
为椭圆![]() 上一点,且
上一点,且![]() ,求三角形
,求三角形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com