
【题目】【2018四川绵阳南山中学高三二诊热身考试】以下四个命题中:
①某地市高三理科学生有15000名,在一次调研测试中,数学成绩![]() 服从正态分布
服从正态分布![]() ,已知
,已知![]() ,若按成绩分层抽样的方式抽取100分试卷进行分析,则应从120分以上(包括120分)的试卷中抽取15分;
,若按成绩分层抽样的方式抽取100分试卷进行分析,则应从120分以上(包括120分)的试卷中抽取15分;
②已知命题![]() ,
,![]() ,则
,则![]() ,
,![]() ;
;
③在![]() 上随机取一个数
上随机取一个数![]() ,能使函数
,能使函数![]() 在
在![]() 上有零点的概率为
上有零点的概率为![]() ;
;
④在某次飞行航程中遭遇恶劣气候,用分层抽样的20名男乘客中有5名晕机,12名女乘客中有8名晕机,在检验这些乘客晕机是否与性别有关时,采用独立性检验,有97%以上的把握认为与性别有关.
| 0.15 | 0.1 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
其中真命题的序号为( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
【答案】B
【解析】对于①,在一次调研测试中,数学成绩ξ服从正态分布N(100,σ2),∴数学成绩ξ关于ξ=100对称,
∵P(80<ξ≤100)=0.40,∴P(ξ>120)=P(ξ<80)=0.5-0.40=0.1,则该班数学成绩在120分以上的人数为0.1×100=10,故①错误;
对于②,已知命题p:x∈R,sinx≤1,则¬p:x∈R,sinx>1,故②正确;
对于③,由(![]() )28≥0,解得m≤-2或m≥2,∴在[-4,3]上随机取一个数m,能使函数
)28≥0,解得m≤-2或m≥2,∴在[-4,3]上随机取一个数m,能使函数![]() 在R上有零点的概率为
在R上有零点的概率为![]() ,故③正确;
,故③正确;
对于④,填写2×2列联表如下:
晕机 | 不晕机 | 合计 | |
男乘客 | 5 | 15 | 20 |
女乘客 | 8 | 4 | 12 |
合计 | 13 | 19 | 32 |
则k2的观测值k=![]() 有97%以上的把握认为晕机与性别有关.故④对
有97%以上的把握认为晕机与性别有关.故④对
故选B


科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=|2x+1|﹣|2x﹣3|,g(x)=|x+1|+|x﹣a|.
(l)求f(x)≥1的解集;
(2)若对任意的t∈R,s∈R,都有g(s)≥f(t).求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856331)
甲、乙两家快餐店对某日7个时段的光顾的客人人数进行统计并绘制茎叶图如下图所示(下面简称甲数据、乙数据),且乙数据的众数为17,甲数据的平均数比乙数据平均数少2.
(Ⅰ)求a,b的值,并计算乙数据的方差;
(Ⅱ)现从乙数据中不大于16的数据中随机抽取两个,求至少有一个数据小于10的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为A的函数f(x),若对任意的x1,x2∈A,都有f(x1+x2)-f(x1)≤f(x2),则称函数f(x)为“定义域上的M函数”,给出以下五个函数:
①f(x)=2x+3,x∈R;②f(x)=x2,x∈![]() ;③f(x)=x2+1,x∈
;③f(x)=x2+1,x∈![]() ;④f(x)=sin x,x∈
;④f(x)=sin x,x∈![]() ;⑤f(x)=log2x,x∈[2,+∞).
;⑤f(x)=log2x,x∈[2,+∞).
其中是“定义域上的M函数”的有( )
A. 2个 B. 3个
C. 4个 D. 5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,若f(x)≥2ln x在[1,+∞)上恒成立,则a的取值范围是( )
,若f(x)≥2ln x在[1,+∞)上恒成立,则a的取值范围是( )
A. (1,+∞) B. [1,+∞)
C. (2,+∞) D. [2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的五面体![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 是正方形,二面角
是正方形,二面角![]() 的大小为
的大小为![]() .
.
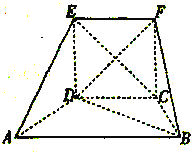
(1)在线段![]() 上找出一点
上找出一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】全集![]() ,非空集合
,非空集合![]() ,且
,且![]() 中的点在平面直角坐标系
中的点在平面直角坐标系![]() 内形成的图形关于
内形成的图形关于![]() 轴、
轴、![]() 轴和直线
轴和直线![]() 均对称.下列命题:
均对称.下列命题:
①若![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() 中至少有8个元素;
中至少有8个元素;
③若![]() ,则
,则![]() 中元素的个数一定为偶数;
中元素的个数一定为偶数;
④若![]() ,则
,则![]() .
.
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com