
【题目】我国古代在珠算发明之前多是用算筹为工具来记数、列式和计算的.算筹实际上是一根根相同长度的小木棍,如图,算筹表示数1~9的方法有两种,即“纵式”和“横式”,规定个位数用纵式,十位数用横式,百位数用纵式,千位数用横式,万位数用纵式……依此类推,交替使用纵横两式.例如:27可以表示为“![]() ”.如果用算筹表示一个不含“0”的两位数,现有7根小木棍,能表示多少个不同的两位数( )
”.如果用算筹表示一个不含“0”的两位数,现有7根小木棍,能表示多少个不同的两位数( )
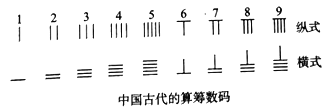
A.54B.57C.65D.69
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为![]() ,据此解答如下问题.
,据此解答如下问题.
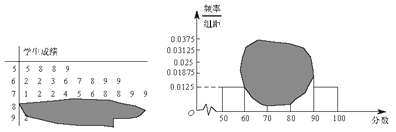
(Ⅰ)求全班人数及分数在![]() 之间的频率;
之间的频率;
(Ⅱ)现从分数在![]() 之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在
之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在![]() 的份数为
的份数为![]() ,求
,求![]() 的分布列和数学望期.
的分布列和数学望期.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右焦点为
的右焦点为![]() ,离心率
,离心率![]() .
.
(1)求椭圆C的标准方程;
(2)已知动直线l过点F,且与椭圆C交于A,B两点,试问x轴上是否存在定点M ,使得![]() 恒成立?若存在,求出点M的坐标,若不存在,请说明理由.
恒成立?若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“辛卜生公式”给出了求几何体体积的一种计算方法:夹在两个平行平面之间的几何体,如果被平行于这两个平面的任何平面所截,截得的截面面积是截面高的(不超过三次)多项式函数,那么这个几何体的体积,就等于其上底面积、下底面积与四倍中截面面积的和乘以高的六分之一.即![]() ,式中
,式中![]() ,
,![]() ,
,![]() ,
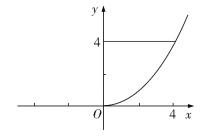
,![]() 依次为几何体的高、上底面积、下底面积、中截面面积.如图,现将曲线
依次为几何体的高、上底面积、下底面积、中截面面积.如图,现将曲线![]() 与直线
与直线![]() 及
及![]() 轴围成的封闭图形绕
轴围成的封闭图形绕![]() 轴旋转一周得到一个几何体,则利用辛卜生公式可求得该几何体的体积为( )
轴旋转一周得到一个几何体,则利用辛卜生公式可求得该几何体的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.16
D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
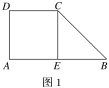
【题目】已知如图1直角梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,E为
,E为![]() 的中点,沿
的中点,沿![]() 将梯形
将梯形![]() 折起(如图2),使平面
折起(如图2),使平面![]() 平面
平面![]() .
.
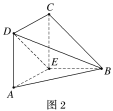
(1)证明:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点F,使得平面
上是否存在点F,使得平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() ,若存在,求出点F的位置;若不存在,请说明理由.
,若存在,求出点F的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且
且![]() .
.
(1)求证:数列![]() 为等差数列;
为等差数列;
(2)若![]() ,且数列
,且数列![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,数列
,数列![]() 满足:
满足:![]() 对于任意给定的正整数
对于任意给定的正整数![]() ,是否存在
,是否存在![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 的值(只要写出一组即可);若不存在,说明理由.
的值(只要写出一组即可);若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com