
【题目】对于下列命题:①对于实数![]() ,若
,若![]() ,则
,则![]() ;②
;②![]() 是
是![]() 的充分而不必要条件;③在(增减算法统宗》中有这样一则故事: 三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关“则此人第二天走了九十六里路;④设函数
的充分而不必要条件;③在(增减算法统宗》中有这样一则故事: 三百七十八里关,初行健步不为难;次日脚痛减一半,如此六日过其关“则此人第二天走了九十六里路;④设函数![]() 的定又域为R,若存在常数:
的定又域为R,若存在常数:![]() ,使
,使![]() 对一切实数x均成立、则称
对一切实数x均成立、则称![]() 为“倍约束函数,所以函数
为“倍约束函数,所以函数![]() 为"倍约束函数”其中所有真命题的序号是_____________.
为"倍约束函数”其中所有真命题的序号是_____________.
科目:高中数学 来源: 题型:
【题目】2019年某开发区一家汽车生产企业计划引进一批新能源汽车制造设备,通过市场分析,全年需投入固定成本3000万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且 ,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
(1)求出2019年的利润![]() (万元)关于年产量x(百辆)的函数关系式;(利润=销售额
(万元)关于年产量x(百辆)的函数关系式;(利润=销售额![]() 成本)
成本)
(2)2019年产量为多少(百辆)时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖促销活动,规定每位顾客从装有0、1、2、3的四个相同小球的抽奖箱中,每次取出一球记下编号后放回(连续取两次),若取出的两个小球的编号相加之和等于6,则中一等奖,等于5中二等奖,等于4或3中三等奖,则顾客抽奖中三等奖的概率为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由中央电视台综合频道![]() 和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了
和唯众传媒联合制作的《开讲啦》是中国首档青年电视公开课.每期节目由一位知名人士讲述自己的故事,分享他们对于生活和生命的感悟,给予中国青年现实的讨论和心灵的滋养,讨论青年们的人生问题,同时也在讨论青春中国的社会问题,受到青年观众的喜爱,为了了解观众对节目的喜爱程度,电视台随机调查了![]() 、
、![]() 两个地区的100名观众,得到如下的
两个地区的100名观众,得到如下的![]() 列联表,已知在被调查的100名观众中随机抽取1名,该观众是
列联表,已知在被调查的100名观众中随机抽取1名,该观众是![]() 地区当中“满意”的观众的概率为0.15.
地区当中“满意”的观众的概率为0.15.

(1)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“满意”的![]() 、
、![]() 地区的人数各是多少;
地区的人数各是多少;
(2)在(1)的条件下,从抽取到“满意”的人中随机抽取2人,设“抽到的观众来自不同的地区”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(3)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系.
的把握认为观众的满意程度与所在地区有关系.

附:参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四边形![]() 中,
中,![]() ,且
,且![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,如图(1),将其沿
,如图(1),将其沿![]() 折起使得平面
折起使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,连接
,连接![]() ,如图(2).
,如图(2).
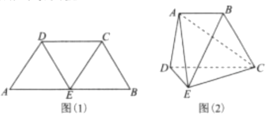
(1)证明:图(2)中的![]() 四点共面;
四点共面;
(2)求图(2)中平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N*,存在实数x使f(x)<2成立.
(1)求实数m的值;
(2)若α≥1,β≥1,f(α)+f(β)=4,求证:![]() ≥3.
≥3.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com